
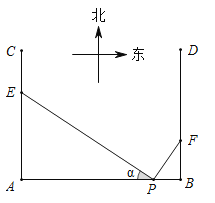
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()
![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
【答案】(1) 当![]() km,
km,![]() km时,
km时,![]() 与
与![]() 的面积之和最小.
的面积之和最小.
(2) 当![]() 为
为![]() ,且
,且![]() 为
为![]() 时,
时,![]() 的值最小.
的值最小.
【解析】
试题分析:(1)用角![]() 表示
表示![]() ,从而表示三角形
,从而表示三角形![]() 的面积,求出面积之和用基本不等式求最小值,求出等号成立时的
的面积,求出面积之和用基本不等式求最小值,求出等号成立时的![]() ,即可确定
,即可确定![]() 的位置;
的位置;
(2) 用角![]() 表示
表示![]() ,构建函数
,构建函数![]() ,用导数与最值的关系求之即可.
,用导数与最值的关系求之即可.
试题解析:(1)在Rt△PAE中,由题意可知![]() ,AP=8,则
,AP=8,则![]() .
.
所以![]() . 2分
. 2分
同理在Rt△PBF中,![]() ,PB=1,则
,PB=1,则![]() ,
,
所以![]() . 4分
. 4分
故△PAE与△PFB的面积之和为![]() 5分
5分
![]() =8,
=8,
当且仅当![]() ,即
,即![]() 时,取“=”,
时,取“=”,
故当![]() km,
km,![]() km时,
km时,![]() 与
与![]() 的面积之和最小. 6分
的面积之和最小. 6分
(2)在Rt△PAE中,由题意可知![]() ,则
,则![]() .
.
同理在Rt△PBF中,![]() ,则
,则![]() .
.
令![]() ,
,![]() , 8分
, 8分
则![]() , 10分
, 10分
令![]() ,得
,得![]() ,记
,记![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调减;
单调减;
当![]() 时,
时,![]() ,
,![]() 单调增.
单调增.
所以![]() 时,
时,![]() 取得最小值, 12分
取得最小值, 12分
此时![]() ,
,![]() .
.
所以当![]() km,且
km,且![]() km时,PE+PF的值最小. 14分
km时,PE+PF的值最小. 14分


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过椭圆的焦点且与长轴垂直的弦长为1.
,过椭圆的焦点且与长轴垂直的弦长为1.
(1)求椭圆C的方程;
(2)设点M为椭圆上第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到点
到点![]() 的距离,等于它到直线
的距离,等于它到直线![]() 的距离.
的距离.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .
.
设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分)一家公司计划生产某种小型产品的月固定成本为![]() 万元,每生产
万元,每生产![]() 万件需要再投入
万件需要再投入![]() 万元.设该公司一个月内生产该小型产品
万元.设该公司一个月内生产该小型产品![]() 万件并全部销售完,每万件的销售收入为
万件并全部销售完,每万件的销售收入为![]() 万元,且每万件国家给予补助
万元,且每万件国家给予补助![]() 万元. (
万元. (![]() 为自然对数的底数,
为自然对数的底数,![]() 是一个常数.)
是一个常数.)
(Ⅰ)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(Ⅱ)当月生产量在![]() 万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).
万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量值(万件). (注:月利润=月销售收入+月国家补助-月总成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )且函数
)且函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)是否存在这样的实数![]() ,使
,使![]() 对所有的
对所有的![]() 均成立?若存在,求出适合条件的实数
均成立?若存在,求出适合条件的实数![]() 的值或范围;若不存在,说明理由.
的值或范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC—A1B1C1中,CA=CB=4,![]() ,E,F分别为AC,CC1的中点,则直线EF与平面AA1B1B所成的角是
,E,F分别为AC,CC1的中点,则直线EF与平面AA1B1B所成的角是
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com