
【题目】有7本不同的书:
(1)全部分给6个人,每人至少一本,有多少种不同的分法?
(2)全部分给5个人,每人至少一本,有多少种不同的分法?.
【答案】(1)15120; (2)16800.
【解析】
(1)根据题意,则分2步进行①、将7本书,分为6组,其中1组2本,其他组每组1本,②、将6组进行全排列对应6人即可;分别求出每一步的情况数目,由分步计数原理计算可得答案.
(2)由题意知7本不同的书分给5个人,每人至少一本,并且全部分完,分两种分法:一人得3本,其余4人各得一本;两人各得2本,其余3人各得一本;分别求出再相加.
(1)根据题意,将7本书分给6个人,且每人至少一本,则必须是其中1个人2本,其他人每人1本,则分2步进行
①、将7本书,分为6组,其中1组2本,其他组每组1本,有![]() 种分组方法,
种分组方法,
②、将分好的6组对应6人,将6组进行全排列即可,有![]() 种方法,
种方法,
则一共有![]() 种不同的分法;
种不同的分法;
(2)有两类办法:一人得3本,其余4人各得一本,方法数为![]() ;
;
两人各得2本,其余3人各得一本,方法数为![]() ,
,
所以所求方法种数为![]() +
+![]() =16800种.
=16800种.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是_________.
(1)命题“若![]() ,则方程
,则方程![]() 有实数根”的逆否命题为“若方程
有实数根”的逆否命题为“若方程![]() 无实数根,则
无实数根,则![]() ”.
”.
(2)命题“![]() ,
,![]() ”的否定“
”的否定“![]() ,
,![]() ”.
”.
(3)若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题.
均为假命题.
(4)“![]() ”是“直线
”是“直线![]() :
:![]() 与直线
与直线![]() :
:![]() 平行”的充要条件.
平行”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点
的中心在原点![]() ,焦点在
,焦点在![]() 轴上,
轴上,![]() 为椭圆
为椭圆![]() 短轴的一个端点,
短轴的一个端点,![]() 、
、![]() 为椭圆的左、右焦点,线段
为椭圆的左、右焦点,线段![]() 的延长线与椭圆
的延长线与椭圆![]() 相交于点
相交于点![]() ,且
,且![]() .
.
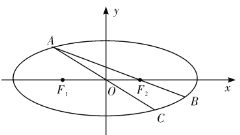
(1)求椭圆![]() 的方程;
的方程;
(2)如图,点![]() 为椭圆上一动点(非长轴端点),
为椭圆上一动点(非长轴端点),![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,
点,![]() 的延长线与椭圆交于
的延长线与椭圆交于![]() 点,求
点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求实数
垂直,求实数![]() 的取值;
的取值;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)记![]() .当
.当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果园基地培育出一种特色水果,要在某一季节内采摘一批这种水果销往A市,每售出1吨这种水果获利800元,未售出的水果每吨亏损400元,根据去年市场调研数据统计,该季节A市对这种水果的市场需求量t(单位:吨,100≤t≤150)的频率分布直方图如图所示.现该果园计划采摘140吨这种水果运往A市,经销这种水果的利润Q(单位:元)

(1)求Q关t的函数表达式;
(2)视频率为概率,求利润Q的分布列及数学期望.(每组数据以区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最近上映的电影《后来的我们》引起了一阵热潮,为了了解大众对这部电影的评价,随机访问了50名观影者,根据这50人对该电影的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,…,
,…,![]() ,
,![]() .
.

(1)求频率分布直方图中![]() 的值,并估计观影者对该电影评分不低于80的概率;
的值,并估计观影者对该电影评分不低于80的概率;
(2)由频率分布直方图估计评分的中位数(保留两位小数)与平均数;
(3)从评分在![]() 的观影者中随机抽取2人,求至少有一人评分在
的观影者中随机抽取2人,求至少有一人评分在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com