
解析:本题的运算量较大,如果直接用普通方程来求解,其计算量会更大,同学们不妨一试.
解:设A、B关于直线l的对称点分别为A1、B1,由对称性知∠A1OB1=∠AOB=90°,由抛物线的参数方程可设A1(2pt12,2pt1)(t1<0),B1(2pt22,2pt2),?
又OA1=OA=1,OB1=OB=8,则有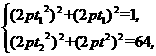 两式相除得
两式相除得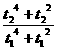 =64.?
=64.?
又∵kOA1=![]() ,kOB1=
,kOB1=![]() ,OA1⊥OB1,?
,OA1⊥OB1,?
∴k OA1·kOB1=-1,即t1·t2=-1.
则可将t2=-![]() 代入上式,得t16=
代入上式,得t16=![]() ,t1=-
,t1=-![]() .?
.?
故有2p=![]() .?
.?
∴A1(![]() ,-2
,-2![]() ).∴kAA1=
).∴kAA1=![]() ,kl=
,kl=![]() .?
.?
故所求直线l的方程为y=![]() 2x,抛物线C的方程为y2=
2x,抛物线C的方程为y2=![]() x.
x.


科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:1994年全国统一高考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com