
分析 (1)利用分类讨论思想和排列组合知识能求出共有多少种分派方法.
(2)设璧山中学分到两名教师为事件A,利用等可能事件概率计算公式能求出璧山中学分到两名教师的概率.
(3)由题意知X的可有取值为1,2,3,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)∵有五名教师被随机的分到49中学、璧山中学、礼嘉中学,且每个中学至少一名教师,
∴共有N=$\frac{1}{2}{C}_{5}^{2}{C}_{3}^{2}{A}_{3}^{3}+{C}_{5}^{3}{A}_{3}^{3}$=150种分派方法.
(2)设璧山中学分到两名教师为事件A,
则P(A)=$\frac{{C}_{5}^{2}{C}_{3}^{2}{A}_{2}^{2}}{\frac{1}{2}{C}_{5}^{2}{C}_{3}^{2}{A}_{3}^{3}+{C}_{3}^{3}{A}_{3}^{3}}$=$\frac{2}{5}$.
(3)由题意知X的可有取值为1,2,3,
P(X=1)=$\frac{{C}_{5}^{1}({C}_{4}^{2}{C}_{2}^{2}+{C}_{4}^{3}{A}_{2}^{2})}{\frac{1}{2}{C}_{5}^{2}{C}_{3}^{2}{A}_{3}^{3}+{C}_{5}^{3}{A}_{3}^{3}}$=$\frac{7}{15}$,
P(X=2)=$\frac{2}{5}$,
P(X=3)=$\frac{{C}_{5}^{2}{A}_{2}^{2}}{\frac{1}{2}{C}_{5}^{2}{C}_{3}^{2}{A}_{3}^{3}+{C}_{5}^{3}{A}_{3}^{3}}$=$\frac{2}{15}$,
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{7}{15}$ | $\frac{2}{5}$ | $\frac{2}{15}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | X1 | X2 | X3 | … | Xn |
| P | p1 | p2 | p3 | … | pn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
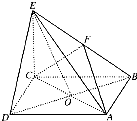 四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.
四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE中点.CE=2,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 命题“?x∈R,x2+2x-1<0”的否定是“?x∈R,x2+2x-1>0” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 若“p或q”为真命题,则p,q至少有一个为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | fs(9)=fT(1) | B. | fs(8)=fT(1) | C. | fs(6)=fT(4) | D. | fs(5)=fT(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com