已知函数f(x)=x2(x-a),其中a∈R.g(x)=f(x)+f'(x).
(I)当函数f(x)的图象在点(1,f(1))处的切线斜率为2时,求此直线在y轴上的截距;
(II)求证:g(x)既有极大值又有极小值;
(III)若g(x)取极大值和极小值对应的x值分别在区间(-2,-1)和(3,4)内,求实数a的取值范围.
【答案】
分析:(I)求出f(x)的导函数,求出f'(1)=3-2a,令其为2求出a的值,写出切线的方程,令方程中的x=0得到直线在y轴上的截距.
(II)求出g′(x)=3x
2-2ax+6x-2a,得到其判别式大于0恒成立,即证得g(x)既有极大值又有极小值
(III)根据题意得到g′(x)=3x
2-2ax+6x-2a的根的分布情况,结合二次函数图象列出不等式,求出a的范围.
解答:解:(I)f(x)=x
2(x-a)=x
3-ax
2
f'(x)=3x
2-2ax,
所以所以3-2a=2得

所以f(1)=

所以切线的方程为4x-2y-3=0
令x=0得
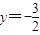
所以此直线在y轴上的截距为

.
(II)因为g(x))=x
3-ax
2+3x
2-2ax
所以g′(x)=3x
2-2ax+6x-2a
△=4a
2+36>0
所以g′(x)=3x
2-2ax+6x-2a有两个不等根,
所以g(x)既有极大值又有极小值;
(III)因为g(x)取极大值和极小值对应的x值分别在区间(-2,-1)和(3,4)内,
所以
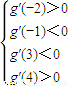
即
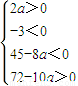
解之得
 点评:
点评:解决函数的性质问题,常借助导数,利用导数求曲线的切线时,一定注意函数在切点处的导数值为曲线的切线的斜率.



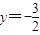
 .
.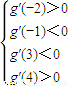 即
即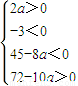



 智能训练练测考系列答案
智能训练练测考系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<