
【题目】甲、乙、丙三人准备报考某大学,假设甲考上的概率为 ![]() ,甲,丙两都考不上的概率为
,甲,丙两都考不上的概率为 ![]() ,乙,丙两都考上的概率为
,乙,丙两都考上的概率为 ![]() ,且三人能否考上相互独立.
,且三人能否考上相互独立.
(1)求乙、丙两人各自考上的概率;
(2)设X表示甲、乙、丙三人中考上的人数与没考上的人数之差的绝对值,求X的分布列与数学期望.
【答案】
(1)解:设A表示“甲考上”,B表示“乙考上”,C表示“丙考上”,
则P(A)= ![]() ,且
,且  ,
,
解得P(C)= ![]() ,P(B)=
,P(B)= ![]() .
.
∴乙考上的概率为 ![]() ,丙考上的概率为
,丙考上的概率为 ![]() .
.
(2)解:由题意X的可能取值为1,2,
P(X=1)= ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
∴X的分布列为:
X | 1 | 2 |
P |
|
|
EX= ![]() =
= ![]() .
.
【解析】(1)设A表示“甲考上”,B表示“乙考上”,C表示“丙考上”,由已知条件利用对立事件概率计算公式和相互独立事件概率乘法公式能求出乙、丙两人各自考上的概率.(2)由题意X的可能取值为1,3,分别求出相应的概率,由此能求出X的分布列和期望.
【考点精析】根据题目的已知条件,利用离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】设全集为实数集R,A={x|3≤x<7},B={x| ![]() ≤2x≤8},C={x|x<a}.
≤2x≤8},C={x|x<a}.
(1)求R(A∪B)
(2)如果A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益函数为R(x)= 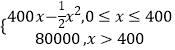 ,其中x是仪器的产量(单位:台);
,其中x是仪器的产量(单位:台);
(1)将利润f(x)表示为产量x的函数(利润=总收益﹣总成本);
(2)当产量x为多少台时,公司所获利润最大?最大利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在直角坐标系![]() 中圆C的参数方程为
中圆C的参数方程为![]() (
(![]() 为参数),以原点O为极点,
为参数),以原点O为极点, ![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求圆C的直角坐标方程及其圆心C的直角坐标;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式中,所得数值最小的是( )
A.sin50°cos39°﹣sin40°cos51°
B.﹣2sin240°+1
C.2sin6°cos6°
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+ ![]() ),则下列结论正确的是( )
),则下列结论正确的是( ) 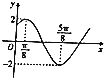
A.函数g(x)的奇函数
B.函数f(x)与g(x)的图象均关于直线x=﹣ ![]() π对称
π对称
C.函数f(x)与g(x)的图象均关于点(﹣ ![]() ,0)对称
,0)对称
D.函数f(x)与g(x)在区间(﹣ ![]() ,0)上均单调递增
,0)上均单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求证:直线DE∥平面A1C1F;
(2) 求证:平面B1DE⊥平面A1C1F.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com