
分析 令t=log${\;}_{\frac{1}{2}}$x,可得y=t2-2t=(t-1)2-1.再利用对数函数、二次函数的单调性的性质,求得函数y的单调区间.
解答 解:令t=log${\;}_{\frac{1}{2}}$x,可得y=t2-2t=(t-1)2-1.
由于函数t在(0,+∞)上是减函数,关于t的二次函数y的图象的对称轴为t=1,
故在区间(0,$\frac{1}{2}$)上,t∈(1,+∞),函数y=(log${\;}_{\frac{1}{2}}$x)2-2log${\;}_{\frac{1}{2}}$x为减函数;
在[$\frac{1}{2}$,+∞),t∈(-∞,1],函数y=(log${\;}_{\frac{1}{2}}$x)2-2log${\;}_{\frac{1}{2}}$x为增函数,
故函数y的减区间为(0,$\frac{1}{2}$),增区间为[$\frac{1}{2}$,+∞).
点评 本题主要考查复合函数的单调性,对数函数、二次函数的性质,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 5+2$\sqrt{2}$ | B. | 2 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{3}$] | B. | [-1,1] | C. | [-$\frac{1}{3}$,+∞) | D. | [-$\frac{4}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 评分等级 | [0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
| 男(人数) | 2 | 5 | 9 | 5 | 4 |
| 女(人数) | 1 | 2 | 5 | 10 | 7 |
| 满意 | 不满意 | 总计 | |
| 男 | 16 | 9 | 25 |
| 女 | 8 | 17 | 25 |
| 总计 | 24 | 26 | 50 |
| P=(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{2}{3}π$) | B. | ($\frac{π}{6}$,$\frac{5}{6}π$) | C. | [$\frac{π}{3}$,$\frac{5}{6}π$) | D. | ($\frac{5}{6}π$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
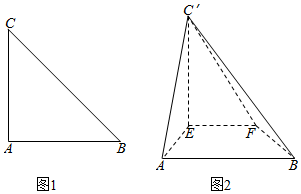 如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′-ABFE
如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′-ABFE查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com