【题目】某工厂计划出售一种产品，经销人员并不是根据生产成本来确定这种产品的价格，而是通过对经营产品的零售商对于不同的价格情况下他们会进多少货进行调查，通过调查确定了关系式P=-750x+15000，其中P为零售商进货的数量（单位：件），x为零售商支付的每件产品价格（单位：元）．现估计生产这种产品每件的材料和劳动生产费用为4元，并且工厂生产这种产品的总固定成本为7000元（固定成本是除材料和劳动费用以外的其他费用），为获得最大利润，工厂应对零售商每件收取多少元？并求此时的最大利润．
科目：高中数学 来源： 题型：
【题目】执行如图所示的程序框图，则“3＜m＜5”是“输出i的值为5”的（ ）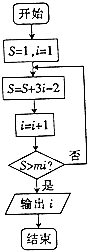 
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分7分）选修4-4：坐标系与参数方程
在平面直角坐标系
中，直线
的参数方程为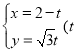
为参数），P、Q分别为直线与x轴、y轴的交点，线段PQ的中点为M．
（Ⅰ）求直线的直角坐标方程；
（Ⅱ）以坐标原点O为极点，
轴的正半轴为极轴建立极坐标系，求点M的极坐标和直线OM的极坐标方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但蔬菜上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水
（单位：千克）清洗蔬菜1千克后，蔬菜上残留的农药
（单位：微克）的统计表：
| 1 | 2 | 3 | 4 | 5 |
| 58 | 54 | 39 | 29 | 10 |
（1）在答题纸的坐标系中，描出散点图，并判断变量
与
是正相关还是负相关；
（2）若用解析式
作为蔬菜农药残量
与用水量
的回归方程，令
，计算平均值
与
，完成以下表格（填在答题卡中），求出
与
的回归方程.（
， 
保留两位有效数字）：
| 1 | 4 | 9 | 16 | 25 |
| 58 | 54 | 39 | 29 | 10 |
| |||||
|
（3）对于某种残留在蔬菜上的农药，当它的残留量低于20微克时对人体无害，为了放心食用该蔬菜，请评估需要用多少千克的清水清洗一千克蔬菜？（精确到0.1，参考数据
）（附：对于一组数据
， 
，……， 
，其回归直线
的斜率和截距的最小二乘法估计分别为： 
， 
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=x2-x+m，且f（log2a）=m，log2f（a）=2，（a≠1）．
（1）求a，m的值；
（2）求f（log2x）的最小值及对应的x的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】国家规定个人稿费缴纳方法为：不超过800元的不纳税，超过800元而不超过4000元的按超过800元部分的14%纳税，超过4000元的按全部稿酬的11.2%纳税（本题中稿费均指纳税前稿费）．
（Ⅰ）某人出了一本书，获得30000元的个人稿费，则这个人需要纳税是多少元？
（Ⅱ）试建立某人所得稿费x元与纳税额y元的函数关系．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在
上的函数
，如果满足：对任意
，存在常数
，都有
成立，则称
是
上的有界函数，其中
称为函数
的一个上界.已知函数
， 
.
（1）若函数
为奇函数，求实数
的值；
（2）在（1）的条件下，求函数
在区间
上的所有上界构成的集合；
（3）若函数
在
上是以3为上界的有界函数，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直角坐标系xOy中，角α的顶点是原点，始边与x轴正半轴重合，终边交单位圆于点A，且
．将角α的终边按逆时针方向旋转
，交单位圆于点B．记A（x1，y1），B（x2，y2）．
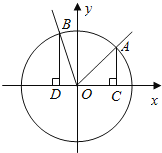
（Ⅰ）若
，求x2；
（Ⅱ）分别过A，B作x轴的垂线，垂足依次为C，D．记△AOC的面积为S1，△BOD的面积为S2．若S1=2S2，求角α的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
