
分析 由已知中$\frac{1}{x-a}$+$\frac{1}{x-b}$+$\frac{1}{x-c}$=0的两根为x1,x2,故$\frac{1}{{x}_{1}-a}+\frac{1}{{x}_{1}-b}+\frac{1}{{x}_{1}-c}=0$,且$\frac{1}{{x}_{2}-a}+\frac{1}{{x}_{2}-b}+\frac{1}{{x}_{2}-c}=0$,进而得到结论.
解答 解:∵$\frac{1}{x-a}$+$\frac{1}{x-b}$+$\frac{1}{x-c}$=0的两根为x1,x2(x1<x2),
∴$\frac{1}{{x}_{1}-a}+\frac{1}{{x}_{1}-b}+\frac{1}{{x}_{1}-c}=0$,且$\frac{1}{{x}_{2}-a}+\frac{1}{{x}_{2}-b}+\frac{1}{{x}_{2}-c}=0$,
故$\frac{1}{{x}_{1}-a},\frac{1}{{x}_{1}-b},\frac{1}{{x}_{1}-c}$至少有一个小于0,又至少一个大于0,
$\frac{1}{{x}_{2}-a},\frac{1}{{x}_{2}-b},\frac{1}{{x}_{2}-c}$至少有一个小于0,又至少一个大于0,
又由a>b>c,x1<x2,得:a>x2>b>x1>c.
点评 本题考查的知识点为不等式的性质,实数的性质,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
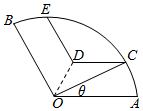 如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.
如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
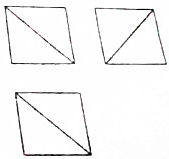 如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )
如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )| A. | 40+8$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 40+16$\sqrt{3}$ | D. | 48+16$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
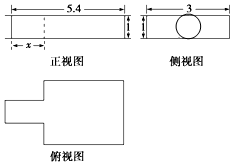 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为( )| A. | 1.2 | B. | 1.6 | C. | 1.8 | D. | 2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∁UN∩M=∅ | B. | ∁UM∩N=∅ | C. | ∁UM∩∁UN=∅ | D. | ∁UM∪∁UN=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
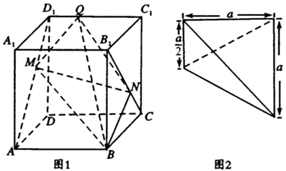
| A. | $\frac{1}{2}{a^3}$ | B. | $\frac{1}{4}{a^3}$ | C. | $\frac{{\sqrt{2}}}{4}{a^3}$ | D. | $\frac{1}{12}{a^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
某班50位学生期中考试数学成绩的频率直方分布图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com