
【题目】已知函数![]() ,
,![]() (其中e为自然对数的底数,m、n为常数),函数
(其中e为自然对数的底数,m、n为常数),函数![]() 定义为:对每一个给定的实数x,
定义为:对每一个给定的实数x,
(1)当m、n满足什么条件时,![]() 对所有的实数x恒成立;
对所有的实数x恒成立;
(2)设a、b是两个实数,满足![]() 且m,
且m,![]() 当
当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间
的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间![]() 的长度定义为
的长度定义为![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意得到![]() 恒成立,从而得到
恒成立,从而得到![]() ,结合绝对值不等式,得到答案;(2)分
,结合绝对值不等式,得到答案;(2)分![]() ,
,![]() ,
,![]() 三种情况进行讨论,根据
三种情况进行讨论,根据![]() 和
和![]() 的图像,得到
的图像,得到![]() 的图像,根据函数图像进行分析,得到答案.
的图像,根据函数图像进行分析,得到答案.
(1)因为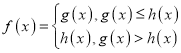 ,
,
所以要得到![]() 对所有的实数x恒成立,
对所有的实数x恒成立,
则![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
则![]() ,取对数得:
,取对数得:![]() 恒成立
恒成立
而![]()
所以![]() 、
、![]() 应满足
应满足![]() ,
,
故![]() 时,
时,![]() 对任意实数x恒成立.
对任意实数x恒成立.
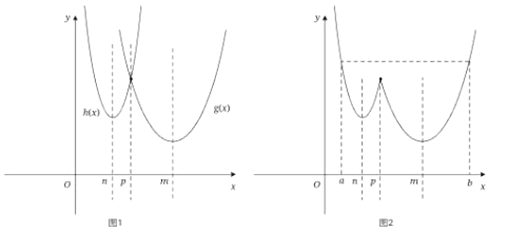
(2)①当![]() 时,
时,![]() ,作出
,作出![]() 和
和![]() 的函数图像,如图
的函数图像,如图![]() 所示,
所示,
根据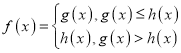 ,可得到
,可得到![]() 图像,如图
图像,如图![]() 所示,
所示,
所以可以得到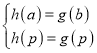 ,
,
即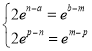 ,即
,即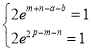 ,
,
所以得到![]() ,
,
![]() ,
,
由图![]() 可知,此时函数
可知,此时函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为
![]()
![]()
![]() ;
;
②当![]() 时,
时,![]() ,作出
,作出![]() 和
和![]() 的函数图像,如图
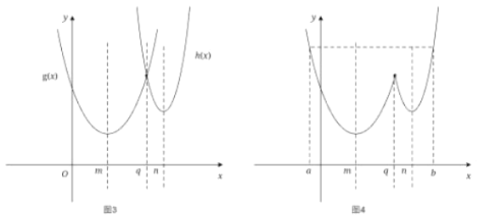
的函数图像,如图![]() 所示,
所示,
根据根据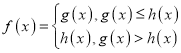 ,可得到
,可得到![]() 图像,如图
图像,如图![]() 所示,
所示,
所以可以得到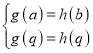 ,
,
即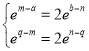 ,即
,即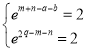 ,
,
所以得到![]() ,
,
![]() ,
,
由图![]() 可知,此时函数
可知,此时函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为
![]()
![]()
![]() ;
;
③当![]() 时,由(1)可知,
时,由(1)可知,![]() ,
,
此时![]() 的函数图像关于直线
的函数图像关于直线![]() 对称,如图
对称,如图![]() 所示,
所示,
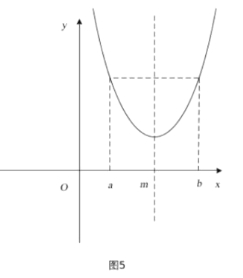
根据对称性可判断,
此时函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为
![]() ,
,
综上所述,函数![]() 在区间
在区间![]() 上的单调增区间的长度之和为
上的单调增区间的长度之和为![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 各条棱的长度均相等,
各条棱的长度均相等,![]() 为
为![]() 的中点,
的中点,![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 的动点(含端点),且满足
的动点(含端点),且满足![]() ,当
,当![]() 运动时,下列结论中不正确的是
运动时,下列结论中不正确的是

A. 在![]() 内总存在与平面
内总存在与平面![]() 平行的线段
平行的线段
B. 平面![]() 平面
平面![]()
C. 三棱锥![]() 的体积为定值
的体积为定值
D. ![]() 可能为直角三角形
可能为直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽
的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽![]() 的进出口,如图2所示.已知旧墙的维修费用为
的进出口,如图2所示.已知旧墙的维修费用为![]() ,新墙的造价为
,新墙的造价为![]() .设利用旧墙的长度为
.设利用旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元).
(单位:元).

(1)将![]() 表示为
表示为![]() 的函数,并写出此函数的定义域;
的函数,并写出此函数的定义域;
(2)若要求用于维修旧墙的费用不得超过修建此矩形场地围墙的总费用的15%,试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:
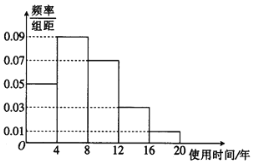
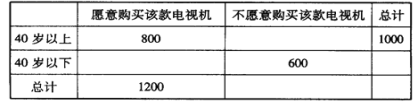
并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在[0,4)和[4,20]的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在[4,20]内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ+ρsinθ=1,曲线C的极坐标方程为ρsin2θ=8cosθ.
(1)求直线l与曲线C的直角坐标方程;
(2)设点M(0,1),直线l与曲线C交于不同的两点P,Q,求|MP|+|MQ|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com