
【题目】如图,在边长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,

(1)求证:CF∥平面A1DE;
(2)求平面A1DE与平面A1DA夹角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)以D为原点,分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角坐标系,利用向量法能证明CF∥平面A1DE.
(2)求出平面A1DE的法向量和平面A1DA的法向量,利用向量法能求出平面A1DE与平面A1DA夹角的余弦值.
证明:(1)以D为原点,分别以DA,DC,DD1为x轴,y轴,z轴建立空间直角坐标系,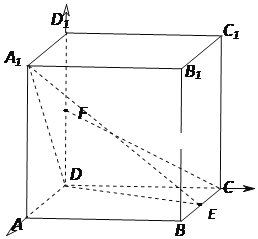
则A(2,0,0),A1(2,0,2),E(1,2,0),D(0,0,0),B1(2,2,2),
则![]() ,
,![]()
设平面A1DE的法向量是![]()
则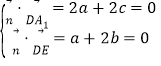 ,取
,取![]() ,
,
∴![]()
所以CF∥平面A1DE.
解:(2)![]() 是面A1DA的法向量,
是面A1DA的法向量,
∴![]()
即平面A1DE与平面A1DA夹角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图231所示.
 图231
图231
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了测量某塔的高度,某人在一条水平公路![]() 两点进行测量.在
两点进行测量.在![]() 点测得塔底
点测得塔底![]() 在南偏西
在南偏西![]() ,塔顶仰角为
,塔顶仰角为![]() ,此人沿着南偏东
,此人沿着南偏东![]() 方向前进10米到
方向前进10米到![]() 点,测得塔顶的仰角为
点,测得塔顶的仰角为![]() ,则塔的高度为( )
,则塔的高度为( )
A. 5米B. 10米C. 15米D. 20米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面向量![]() ,
,![]() 满足:|
满足:|![]() |=2,|
|=2,|![]() |=1.
|=1.
(1)若(![]() 2
2![]() )(
)(![]() )=1,求
)=1,求![]()
![]() 的值;
的值;
(2)设向量![]() ,
,![]() 的夹角为θ.若存在t∈R,使得
的夹角为θ.若存在t∈R,使得![]() ,求cosθ的取值范围.
,求cosθ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,侧面
的菱形,侧面![]() 底面
底面![]() ,
,![]() 60°,
60°, ![]() ,
, ![]() 是
是![]() 中点,点
中点,点![]() 在侧棱
在侧棱![]() 上.
上.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)是否存在![]() ,使平面
,使平面![]()
![]() 平面
平面![]() ?若存在,求出,若不存在,说明理由.
?若存在,求出,若不存在,说明理由.
(Ⅲ)是否存在![]() ,使
,使![]() 平面
平面![]() ?若存在,求出.若不存在,说明理由.
?若存在,求出.若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解甲、乙两班学生的学业水平,从两班中各随机抽取![]() 人参加学业水平等级考试,得到学生的学业成绩茎叶图如图:
人参加学业水平等级考试,得到学生的学业成绩茎叶图如图:

(Ⅰ)通过茎叶图比较甲、乙两班学生的学业成绩平均值![]() 与
与![]() 及方差
及方差![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅱ)根据学生的学业成绩,将学业水平分为三个等级:

根据所给数据,频率可以视为相应的概率.
(i)从甲、乙两班中各随机抽取![]() 人,记事件
人,记事件![]() :“抽到的甲班学生的学业水平高于乙班学生的学业水平等级”,求
:“抽到的甲班学生的学业水平高于乙班学生的学业水平等级”,求![]() 发生的概率;
发生的概率;
(ii)从甲班中随机抽取![]() 人,记
人,记![]() 为学业水平优秀的人数,求
为学业水平优秀的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据: ![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按规定:车辆驾驶员血液酒精浓度在20—80mg/100ml(不含80)之间,属酒后驾车;在![]() (含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,右图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.
(含80)以上时,属醉酒驾车.某市交警在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后驾车和醉酒驾车的驾驶员20人,右图是对这20人血液中酒精含量进行检查所得结果的频率分布直方图.

(1)根据频率分布直方图,求:此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在![]() 范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com