
【题目】如图,五面体![]() 中,
中,![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上靠近
上靠近![]() 的三等分点.
的三等分点.
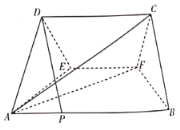
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)分别取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,证明出
,证明出![]() ,可得出
,可得出![]() 平面
平面![]() ,证明出
,证明出![]() ,可得出
,可得出![]() 平面
平面![]() ,利用面面平行的判定定理可得出平面
,利用面面平行的判定定理可得出平面![]() 平面
平面![]() ,由此可得出
,由此可得出![]() 平面
平面![]() ;
;
(2)以![]() 为原点,
为原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴,以过点
轴,以过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设
,设![]() ,利用空间向量法可计算出直线
,利用空间向量法可计算出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)如图,分别取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() .
.
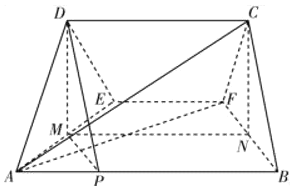
由题可知![]() ,
,![]() .
.
设![]() ,易知
,易知![]() ,且
,且![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() ,由余弦定理得
,由余弦定理得![]() ,
,
![]() ,所以
,所以![]() ,
,
所以![]() 是以
是以![]() 为斜边的等腰直角三角形,所以
为斜边的等腰直角三角形,所以![]() ,
,
而![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)如图,连接![]() ,以
,以![]() 为原点,
为原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴,以过点
轴,以过点![]() 且垂直于平面
且垂直于平面![]() 的直线为
的直线为![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
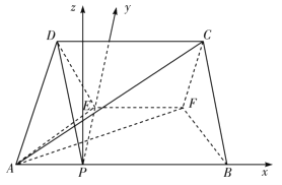
设![]() ,则
,则![]() ,
,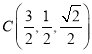 ,
,![]() ,
,![]() ,
,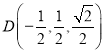 ,所以
,所以![]() ,
,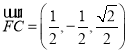 .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则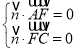 ,即
,即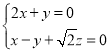 ,
,
取![]() ,则
,则![]() ,
,![]() ,即
,即![]() .
.
易知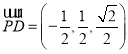 ,设直线
,设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
故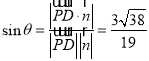 ,即直线
,即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
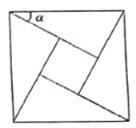
【题目】“剑桥学派”创始人之一数学家哈代说过:“数学家的造型,同画家和诗人一样,也应当是美丽的”;古希腊数学家毕达哥拉斯创造的“黄金分割”给我们的生活处处带来美;我国古代数学家赵爽创造了优美“弦图”.“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于![]() 分的选手定为合格选手,直接参加第二轮比赛,大于等于
分的选手定为合格选手,直接参加第二轮比赛,大于等于![]() 分的选手将直接参加竞赛选拔赛.已知成绩合格的
分的选手将直接参加竞赛选拔赛.已知成绩合格的![]() 名参赛选手成绩的频率分布直方图如图所示,其中
名参赛选手成绩的频率分布直方图如图所示,其中![]() 的频率构成等比数列.
的频率构成等比数列.
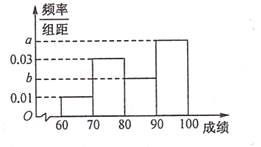
(1)求![]() 的值;
的值;
(2)估计这![]() 名参赛选手的平均成绩;
名参赛选手的平均成绩;
(3)根据已有的经验,参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为![]() ,假设每名选手能否通过竞赛选拔赛相互独立,现有
,假设每名选手能否通过竞赛选拔赛相互独立,现有![]() 名选手进入竞赛选拔赛,记这
名选手进入竞赛选拔赛,记这![]() 名选手在竞赛选拔赛中通过的人数为随机变量
名选手在竞赛选拔赛中通过的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
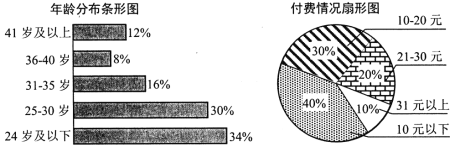
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
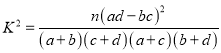 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=BC=4,BB1=2![]() ,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
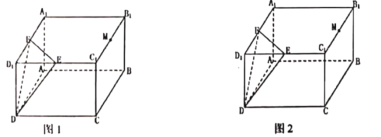
(1)在图1中,画出这个几何图形,并求这个几何图形的面积(不必说明画法与理由)
(2)在图2中,求证:D1B⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是由非负整数组成的无穷数列,对每一个正整数
是由非负整数组成的无穷数列,对每一个正整数![]() ,该数列前
,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() 的最小值记为
的最小值记为![]() ,记
,记![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)证明:“数列![]() 单调递增”是“
单调递增”是“![]() ”的充要条件;
”的充要条件;
(3)若![]() 对任意
对任意![]() 恒成立,证明:数列
恒成立,证明:数列![]() 的通项公式为
的通项公式为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 相交于
相交于![]()
![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com