
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若函数![]() 的值域为
的值域为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 的解集中恰好只有一个元素,求
的解集中恰好只有一个元素,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据对数函数的单调性可解得, 注意真数大于零;
(2) 化简得到![]() 的值域为
的值域为![]() ,故
,故![]() 能够取到一切大于0的实数,由于二次项系数含参,故需要分类讨论,当
能够取到一切大于0的实数,由于二次项系数含参,故需要分类讨论,当![]() 时,显然不符合题意;故只能
时,显然不符合题意;故只能![]() ,再结合
,再结合![]() 即得答案.
即得答案.
(3) 化简对数方程得到![]() ,在
,在![]() 的条件下只有一个根,然后分类讨论即可得到答案.
的条件下只有一个根,然后分类讨论即可得到答案.
(1) ![]() 时,不等式
时,不等式![]() 等价于
等价于![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以不等式![]() 的解集为
的解集为![]() .
.
(2) 因为函数![]() 的值域为
的值域为![]() ,即
,即![]() 的值域为
的值域为![]() ,故
,故![]() 能够取到一切大于0的实数,
能够取到一切大于0的实数,
当![]() 时,
时,![]() ,不符合题意;
,不符合题意;
当![]() 时,
时,
![]()
![]() 不符合题意,
不符合题意,
当![]() 时, 根据二次函数的图象和性质可得
时, 根据二次函数的图象和性质可得![]() ,解得
,解得![]() ;
;
综上所述: ![]() 的取值范围是
的取值范围是![]() .
.
(3) 关于![]() 的方程
的方程![]() 的解集中恰好只有一个元素,
的解集中恰好只有一个元素,
所以![]() 的解集中恰好只有一个元素,
的解集中恰好只有一个元素,
即![]() 且
且![]() 的解集中恰好只有一个元素,
的解集中恰好只有一个元素,
所以![]() ,即
,即![]() ,
,
①当![]() 时,解得
时,解得![]() ,此时
,此时![]() ,满足题意;
,满足题意;
②当![]() 时,
时,![]() ,此时
,此时![]() 也满足题意;
也满足题意;
③当![]() 且
且![]() 时,两根为
时,两根为![]() ,
,![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,
,
因为![]() 和
和![]() 只能取一个值,
只能取一个值,
所以只能取![]() ,所以
,所以![]() 且
且![]() ,
,
解得![]() .
.
综上所述:![]() 的取值范围是
的取值范围是![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)记函数![]() 的导函数是
的导函数是![]() ,若不等式
,若不等式![]() 对任意的实数
对任意的实数![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)设函数![]() ,
,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且
,且![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在已分组的若干数据中,每组的频数是指___________,每组的频率是指____________.
(2)一个公司共有N名员工,下设一些部门,要采用等比例外层随机抽样的方法从全体员工中抽取样本量为n的样本,如果某部门有m名员工,那么从该部门抽取的员工人数是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶某中学一研究性学习小组早晨在校门口询问调查同学的体重,对来校同学依次每5人抽取一人询问体重,共抽取40位同学,将他们的体重(![]() 分成六段:
分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计后得到如图的频率分布直方图.
,统计后得到如图的频率分布直方图.
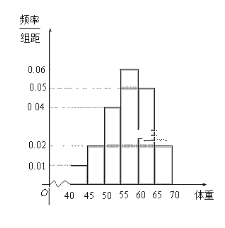
(1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40位同学体重的众数和中位数的估计值.
(2)从体重在![]() 的同学中任意抽取3位,求体重在
的同学中任意抽取3位,求体重在![]() ,
,![]() 内都有同学的概率.
内都有同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,已知成绩在130~140分数段的人数为2.
(1)求这组数据的平均数M.
(2)现根据初赛成绩从第一组和第五组(从低分段至高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶小组.若选出的两人的成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
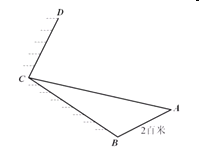
【题目】如图是一景区的截面图,![]() 是可以行走的斜坡,已知
是可以行走的斜坡,已知![]() 百米,
百米,![]() 是没有人行路(不能攀登)的斜坡,
是没有人行路(不能攀登)的斜坡,![]() 是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡
是斜坡上的一段陡峭的山崖.假设你(看做一点)在斜坡![]() 上,身上只携带着量角器(可以测量以你为顶点的角).
上,身上只携带着量角器(可以测量以你为顶点的角).
(1)请你设计一个通过测量角可以计算出斜坡![]() 的长的方案,用字母表示所测量的角,计算出
的长的方案,用字母表示所测量的角,计算出![]() 的长,并化简;
的长,并化简;
(2)设![]() 百米,
百米,![]() 百米,
百米,![]() ,
,![]() ,求山崖
,求山崖![]() 的长.(精确到米)
的长.(精确到米)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com