
【题目】设集合A={y|y=log ![]() x,
x, ![]() },B={x|y=
},B={x|y= ![]() }.
}.
(1)若a=2,求A∩B;
(2)若A∪B=B,求实数a的取值范围.
【答案】
(1)解:∵y=log ![]() x在(0,+∞)上单调递减,且x∈[
x在(0,+∞)上单调递减,且x∈[ ![]() ,2],
,2],
∴log ![]() 2≤y≤
2≤y≤ ![]() ,即﹣1≤y≤3.
,即﹣1≤y≤3.
∴A={y|﹣1≤y≤3},
函数y= ![]() 有意义,则3x﹣a﹣1≥0,解得x≥a.
有意义,则3x﹣a﹣1≥0,解得x≥a.
当a=2时,B={x|x≥2}.
∴A∩B={x|2≤x≤3}
(2)解:由(1)知A={y|﹣1≤y≤3},B={x|x≥a},
由A∪B=B,得AB,∴a≤﹣1,
∴实数a的取值范围是(﹣∞,1]
【解析】(1)当a=2时,利用对数函数的单调性即可求出A={y|﹣1≤y≤3},再根据指数函数的单调性解出x≥a,即得B={x|x≥2}再根据集合的交集定义求出结果。(2)根据题意可得AB利用集合的子集定义结合数轴求出a的取值范围。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,g(x)=x2 . (Ⅰ)求函数h(x)=f(x)﹣x+1的最大值;
(Ⅱ)对于任意x1 , x2∈(0,+∞),且x1<x2 , 是否存在实数m,使mg(x1)﹣mg(x2)﹣x2f(x2)+x1f(x1)恒为正数?若存在,求出m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字). 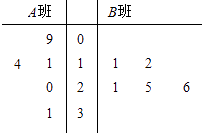
(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(Ⅱ)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题说法正确的是( )
A.命题p:“?x∈R,sinx+cosx= ![]() ”,则?p是真命题
”,则?p是真命题
B.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件
C.命题“?x∈R,使得x2+x+1<0“的否定是:“?x∈R,x2+x+1<0”
D.“a>l”是“y=logax(a>0且a≠1)在(0,+∞)上为增函数”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据所学知识完成题目:
(1)求函数f(x)=2x+4 ![]() 的值域;
的值域;
(2)求函数f(x)= ![]() 的值域.
的值域.
(3)函数f(x)=x2﹣2x﹣3,x∈(﹣1,4]的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com