
【题目】“石头、剪刀、布”是个广为流传的游戏,游戏时甲乙双方每次做“石头”“剪刀”“布”三种手势中的一种,规定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛,假设甲乙两人都是等可能地做这三种手势.
(1)列举一次比赛时两人做出手势的所有可能情况;
(2)求一次比赛甲取胜的概率,并说明“石头、剪刀、布”这个广为流传的游戏的公平性.
科目:高中数学 来源: 题型:
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了![]() 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为![]() 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)设该公司从至少消费两次, 求这的顾客消费次数用分层抽样方法抽出![]() 人, 再从这
人, 再从这![]() 人中抽出
人中抽出![]() 人发放纪念品, 求抽出
人发放纪念品, 求抽出![]() 人中恰有
人中恰有![]() 人消费两次的概率.
人消费两次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些会有缺损,按不同转速生产出来的零件有缺损的统计数据如表所示:

(1)作出散点图;
(2)如果![]() 与
与![]() 线性相关,求出回归直线方程.
线性相关,求出回归直线方程.
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为,
的斜率和截距的最小二乘估计分别为,
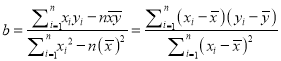 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为2,过右焦点和短轴一个端点的直线的斜率为
的焦距为2,过右焦点和短轴一个端点的直线的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记
两点,记![]() 面积的最大值为
面积的最大值为![]() ,证明:
,证明: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
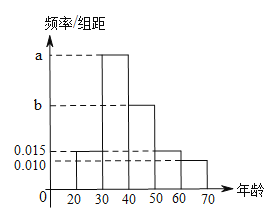
【题目】根据某电子商务平台的调查统计显示,参与调查的![]() 位上网购物者的年龄情况如下图.
位上网购物者的年龄情况如下图.
(1)已知![]() 、
、![]() 、
、![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放![]() 元的代金券,潜在消费人群每人发放
元的代金券,潜在消费人群每人发放![]() 元的代金券.已经采用分层抽样的方式从参与调查的
元的代金券.已经采用分层抽样的方式从参与调查的![]() 位上网购物者中抽取了
位上网购物者中抽取了![]() 人,现在要在这
人,现在要在这![]() 人中随机抽取
人中随机抽取![]() 人进行回访,求此三人获得代金券总和
人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】葫芦岛市某工厂党委为了研究手机对年轻职工工作和生活的影响情况做了一项调查:在厂内用简单随机抽样方法抽取了30名25岁至35岁的职工,对其“每十天累计看手机时间”(单位:小时)进行调查,得到茎叶图如下.所抽取的男职工“每十天累计看手机时间”的平均值和所抽取的女生 “每十天累计看手机时间”的中位数分别是( )
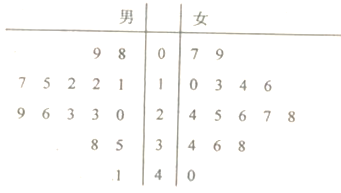
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙、丙、丁、戊、己等6人.(以下问题用数字作答)
(1)邀请这6人去参加一项活动,必须有人去,去几人自行决定,共有多少种不同的情形?
(2)这6人同时加入6项不同的活动,每项活动限1人,其中甲不参加第一项活动,乙不参加第三项活动,共有多少种不同的安排方法?
(3)将这6人作为辅导员安排到3项不同的活动中,每项活动至少安排1名辅导员;求丁、戊、己恰好被安排在同一项活动中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+blog3![]() (其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.
(1)求出a,b的值;
(2)若这种鸟类为赶路程,飞行的速度不能低于2 m/s,则其耗氧量至少要多少个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com