
【题目】已知函数![]()
(1)求曲线![]() 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程;
(2)求经过点A(1,3)的曲线![]() 的切线方程.
的切线方程.
【答案】(1)2x-y+1=0(2)x-y+2=0或2x-y+1=0
【解析】试题分析:(1)求出![]() ,求出
,求出![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(2)设切点坐标为
处的切线方程;(2)设切点坐标为![]() ,求出
,求出![]() 的值,可得切线斜率,利用点斜式可得曲线
的值,可得切线斜率,利用点斜式可得曲线![]() 在点
在点![]() 的切线方程,将
的切线方程,将![]() 代入切线方程可求得
代入切线方程可求得![]() 的值,从而可得结果.
的值,从而可得结果.
试题解析:(1)函数f(x)=x3﹣x2+x+2的导数为f′(x)=3x2﹣2x+1,
可得曲线f(x)在点(1,f(1))处的切线斜率为3﹣2+1=2,
切点为(1,3),
即有曲线f(x)在点(1,f(1))处的切线方程为y﹣3=2(x﹣1),
即为2x﹣y+1=0;
(2)设切点为(m,n),可得n=m3﹣m2+m+2,
由f(x)的导数f′(x)=3x2﹣2x+1,
可得切线的斜率为3m2﹣2m+1,
切线的方程为y﹣(m3﹣m2+m+2)=(3m2﹣2m+1)(x﹣m),
由切线经过点(1,3),可得
3﹣(m3﹣m2+m+2)=(3m2﹣2m+1)(1﹣m),
化为m(m﹣1)2=0,解得m=0或1.
则切线的方程为y﹣2=x或y﹣3=2(x﹣1),
即为y=x+2或y=2x+1.


科目:高中数学 来源: 题型:
【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1= ![]() 且13a2=3S3(n∈N*).
且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=nan , 求数列{bn}的前项n和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】响应“文化强国建设”号召,某市把社区图书阅览室建设增列为重要的民生工程.为了解市民阅读需求,随机抽取市民200人做调查,统计显示,男士喜欢阅读古典文学的有64人,不喜欢的有56人;女士喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导市民积极参与阅读,有关部门牵头举办市读书交流会,从这200人中筛选出5名男代表和4名代表,其中有3名男代表和2名女代表喜欢古典文学.现从这9名代表中任选3名男代表和2名女代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() 过
过 ![]() ,
, ![]() 两点,O为坐标原点
两点,O为坐标原点
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使该圆的任意一条切线与椭圆E 恒有两个交点A、B,且 ![]() ?若存在,写出该圆的方程;若不存在,说明理由.
?若存在,写出该圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(附加题,本小题满分10分,该题计入总分)
已知函数![]() ,若在区间
,若在区间![]() 内有且仅有一个
内有且仅有一个![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)若![]() ,判断
,判断![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,试求实数
,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,则下列结论中正确的是__________.
,则下列结论中正确的是__________.
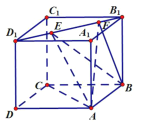
①![]() 平面
平面![]() ;
;
②平面![]() 平面
平面![]() ;
;
③三棱锥![]() 的体积为定值;
的体积为定值;
④存在某个位置使得异面直线![]() 与
与![]() 成角
成角![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com