
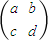 的变换得到新的点P'(x',y')称作一次运动,即:
的变换得到新的点P'(x',y')称作一次运动,即: .
.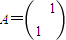 变换后得到新的点P',求出点P'的坐标,并指出点P'与点P的位置关系;
变换后得到新的点P',求出点P'的坐标,并指出点P'与点P的位置关系;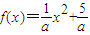 (x≥0)的图象上的每一个点经过(1)中的矩阵A变换后,所得到图象对应函数y=g(x),试研究在y=g(x)上是否存在定义域与值域相同的区间[m,n],若存在,求出满足条件的实数a的取值范围;若不存在,说明理由.
(x≥0)的图象上的每一个点经过(1)中的矩阵A变换后,所得到图象对应函数y=g(x),试研究在y=g(x)上是否存在定义域与值域相同的区间[m,n],若存在,求出满足条件的实数a的取值范围;若不存在,说明理由.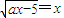 当x≥0时有两个相异实根,即方程ax-5=x2有两个相异正根(x=0显然不是方程的根),从而转化函数y=a与函数
当x≥0时有两个相异实根,即方程ax-5=x2有两个相异正根(x=0显然不是方程的根),从而转化函数y=a与函数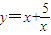 (x>0)有两个交点,故可解.
(x>0)有两个交点,故可解.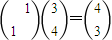 ,∴P'的坐标为(4,3)(2分)
,∴P'的坐标为(4,3)(2分)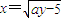 ∴当a>0时,
∴当a>0时,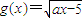 (
(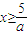 )(7分)
)(7分)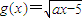 (
(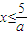 )(8分)
)(8分)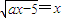 当x≥0时有两个相异实根,(10分)
当x≥0时有两个相异实根,(10分) (x>0)即函数y=a与函数
(x>0)即函数y=a与函数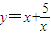 (x>0)有两个交点,
(x>0)有两个交点,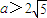 (
(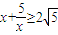 当且仅当
当且仅当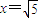 时有最小值)(12分)
时有最小值)(12分)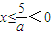 ,∴当a<0时,不存在定义域与值域相同的区间[m,n],∴a的取值范围为
,∴当a<0时,不存在定义域与值域相同的区间[m,n],∴a的取值范围为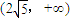 .(14分)
.(14分)

科目:高中数学 来源: 题型:
|
|
|
|
|
| 1 |
| a |
| 5 |
| a |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
|
|
|
|
| 1 |
| a |
| 5 |
| a |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省绍兴一中高三(下)回头考试数学试卷(理科)(解析版) 题型:解答题
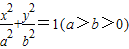 (如图),求证:xE•xF是与MN和点P位置无关的定值;
(如图),求证:xE•xF是与MN和点P位置无关的定值;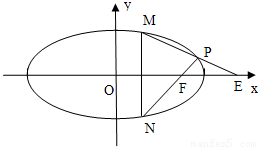
查看答案和解析>>
科目:高中数学 来源:2011年上海市松江区、徐汇区高考数学一模试卷(理科)(解析版) 题型:解答题
 (如图),求证:xE•xF是与MN和点P位置无关的定值;
(如图),求证:xE•xF是与MN和点P位置无关的定值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com