
【题目】已知中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2. 
(1)求椭圆的标准方程;
(2)设P,Q是椭圆上异于点B的任意两点,且BP⊥BQ,线段PQ的中垂线l与x轴的交点为(x0 , 0),求x0的取值范围.
【答案】
(1)解:∵中心在原点O,焦点在x轴上的椭圆的一个顶点为B(0,1),B到焦点的距离为2.
∴由条件:b=1,a=2,
∴椭圆的标准方程为: ![]() =1
=1
(2)解:①当直线PQ斜率k=0时,线段PQ的中垂线l在x轴上的截距为0;
②设PQ:y=kx+m,(k≠0),
则: ![]() ﹣4=0,
﹣4=0,
设P(x1,y1),Q(x2,y2),
则 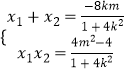 ,
,
∵BP⊥BQ,∴ ![]() ,
,
∴(1+k2)x1x2+k(m﹣1)(x1+x2)+(m﹣1)2=0(1+k2) ![]() =0
=0
∴5m2﹣2m﹣3=0m=﹣ ![]() 或m=1(舍去),
或m=1(舍去),
∴PQ为:y=kx﹣ ![]() ,
,
∴xM= ![]() ,yM=
,yM= ![]() ,
,
∴线段PQ的中垂线l为:y+ ![]() ,
,
∴在x轴上截距x0= ![]() ,
,
∴|x0|= ![]() ,
,
∴﹣ ![]() 且x0≠0,
且x0≠0,
综合①②得:线段PQ的中垂线l在x轴上的截距的取值范围是 ![]()
【解析】(1)由条件b=1,a=2,由此能求出椭圆的标准方程.(2)当直线PQ斜率k=0时,线段PQ的中垂线l在x轴上的截距为0;当k≠0时,设PQ:y=kx+m,取椭圆联立得(1+4k2)x2+8kmx+4m2﹣4=0,由此利用韦达定理、向量垂直、中垂线性质,结合已知条件能求出线段PQ的中垂线l在x轴上的截距的取值范围.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】设F为抛物线C:y2=4x的焦点,过点P(﹣1,0)的直线l交抛物线C于两点A,B,点Q为线段AB的中点,若|FQ|=2,则直线l的斜率等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1 , 则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A1 , A2 , …,An(n≥4)为集合S={1,2,…,n}的n个不同子集,为了表示这些子集,作n行n列的数阵,规定第i行第j列的数为: ![]() .则下列说法中,错误的是( )
.则下列说法中,错误的是( ) 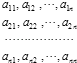
A.数阵中第一列的数全是0当且仅当A1=
B.数阵中第n列的数全是1当且仅当An=S
C.数阵中第j行的数字和表明集合Aj含有几个元素
D.数阵中所有的n2个数字之和不超过n2﹣n+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为( )
A.101
B.808
C.1212
D.2012
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,点A在BD上的射影为O,∠BAD=∠BCD=90°,AB=BC=2,AD=DC=2 ![]() ,AC=
,AC= ![]() .
. 
(1)求证:AO⊥平面BCD;
(2)若E是AC的中点,求直线BE和平面BCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ ![]() ﹣mx(m∈R).
﹣mx(m∈R).
(Ⅰ)当m=﹣1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若f(x)在(0,+∞)上为单调递减,求m的取值范围;
(Ⅲ)设0<a<b,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com