在周长为300cm的圆周上,有甲、乙两球以大小不等的速度作匀速圆周运动.甲球从A点出发按逆时针方向运动,乙球从B点出发按顺时针方向运动,两球相遇于C点.相遇后,两球各自反方向作匀速圆周运动,但这时甲球速度的大小是原来的2倍,乙球速度的大小是原来的一半,以后他们第二次相遇于D点.已知AmC=40厘米,BnD=20厘米,求ACB的长度.
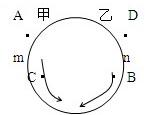
解:如图设BC=x厘米.
甲球速度为v
甲,乙球速度为v
乙.
根据二次从出发到相遇二球运动的时间都相同,
可得第一次等候时方程
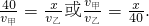
第二次等候时方程

.
由此可得

,
(x-40)(x-80)=0.
由于已知条件v
甲≠v
乙,
∴x≠40,
x=80(厘米)
ACB=40+80=120(厘米).
分析:本题考查的知识点是方程的构造与应用,要求ACB的长度,由AmC=40厘米,我们只要求出BC长即可,我们不妨设BC=x厘米,甲球速度为v
甲,乙球速度为v
乙.然后根据相遇问题中时间相等,构造两次相遇时的方程,解方程组即可求出答案.
点评:方程与函数思想是中学阶段的四大数学思想之一,在利用方程思想解决问题时,我们要解决两个问题:一是谁是未知数,一般由“求谁设谁”的原则来决定;二是找等量关系,如本题中相遇问题的时间相等.并由些构造方程,进行求解.

 解:如图设BC=x厘米.
解:如图设BC=x厘米.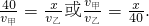
 .
. ,
,
