
已知数列 中,
中, .
.
(1)求证: 是等比数列,并求
是等比数列,并求 的通项公式
的通项公式 ;
;
(2)数列 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)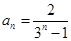 ;(2)
;(2)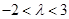 .
.
解析试题分析:本题主要考查数列的证明、错位相减法、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力和计算能力.第一问,将已知的递推公式进行变形,转化出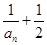 的形式来证明,还可以根据等比数列的定义来证明;第二问,将第一问得到的结论代入,先得到
的形式来证明,还可以根据等比数列的定义来证明;第二问,将第一问得到的结论代入,先得到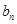 表达式,利用错位相减法,得到数列
表达式,利用错位相减法,得到数列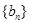 的前n项和
的前n项和 的值,再利用恒成立问题求
的值,再利用恒成立问题求 的值,在最后这一步,需要对n进行讨论,分奇数、偶数两种情况讨论.
的值,在最后这一步,需要对n进行讨论,分奇数、偶数两种情况讨论.
试题解析:(1)由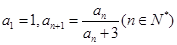 知,
知, ,
,
又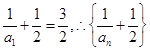 是以
是以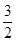 为首项,
为首项,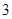 为公比的等比数列,
为公比的等比数列,  6分
6分
(2)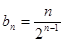 ,
, 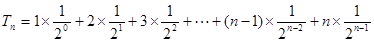
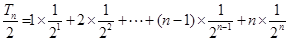 ,
,
两式相减得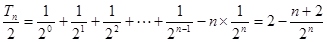 ,
,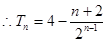 9分
9分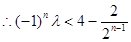 10分
10分
若n为偶数,则 11分
11分
若n为奇数,则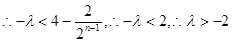 13分
13分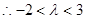 14分
14分
考点:数列的证明、错位相减法、恒成立问题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利a元的前提下,可卖出b件;若做广告宣传,广告费为n千元比广告费为 千元时多卖出
千元时多卖出 件。
件。
(1)试写出销售量 与n的函数关系式;
与n的函数关系式;
(2)当 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,且在点Pn(n,Sn)处的切线的斜率为kn.
(1)求数列{an}的通项公式;
(2)若bn=2knan,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 为公差不为
为公差不为 的等差数列,
的等差数列, 为前
为前 项和,
项和, 和
和 的等差中项为
的等差中项为 ,且
,且 .令
.令 数列
数列 的前
的前 项和为
项和为 .
.
(1)求 及
及 ;
;
(2)是否存在正整数 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com