分析:(I)根据几何体的结构特征得到线面的有关位置关系,即利用线线垂直证明线面垂直再利用直线在另一个平面内进而证明面面垂直.
(II)先由其中一个平面内的一点作另一个平面的垂线,作交线的垂线即作出二面角的平面角,再证明此角是所求交,然后利用解三角形的有关知识解决问题即可.
解答:解:(I)证明:设AC、A
1C
1的中点分别为N、N
1,连接NN1交AC
1于M,连接MD,则NN
1与CC
1平行而且相等,
由已知可得MN=BD,所以BDMN是矩形,
所以DM∥BN.
因为ABC-A
1B
1C
1是直三棱柱,
所以平面ABC⊥平面ACC
1A
1,BN⊥AC,
所以BN⊥平面ACC
1A
1.
所以DM⊥平面ACC
1A
1,
因为DM?平面ADC
1,
所以平面ADC
1⊥平面ACC
1A
1.
(II)因为ABC-A
1B
1C
1是直三棱柱,所以△ABC是△ADC
1在平面ABC内的射影.
设平面ADC1与平面ABC所成二面角(锐角)的大小等于θ,则cosθ=
由已知得
S△ABC=a2,DM=BN=
,AC1=
a,
所以
S△ADC1=×AC1×DM=,
所以cosθ=
=
,(θ为锐角)
所以
θ=arccos.
所以平面ADC
1与平面ABC所成二面角(锐角)的大小为
arccos.
点评:解决此类问题的关键是熟悉几何体的结构特征,根据特征得到线面垂直的有关结论,并且解决二面角的平面角.

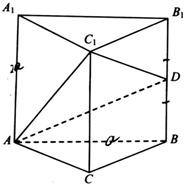 如图,在正三棱柱ABC-A1B1C1中,AB=a,AA1=2a,D是侧棱的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=a,AA1=2a,D是侧棱的中点.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( ) 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.