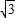Question

已知：f（x）=2acos²x+asin2x+a²（a∈R，a≠0为常数）．
（1）若x∈R，求f（x）的最小正周期；
（2）若，f（x）的最大值大于10，求a的取值范围．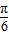

Answer 1

【答案】分析：（1）利用三角函数的恒等变换化简函数f（x）的解析式为2asin（2x+）+a²+a，由此求得函数的最小正周期．
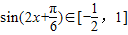（2）根据x的范围求出，当a＞0时，由最大值大于10，求出a的范围，当a＜0时，同理由最大值大于10，求出a的范围，再把a的范围取并集，即得所求．
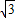解答：解：（1）f（x）=a（1+cos2x）+asin2x+a² =2a（sin2xcos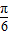+cos2xsin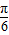）+a²+a=2asin（2x+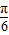）+a²+a，…（3分）
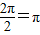所以函数的最小正周期为T=．…（4分）
（2）∵，
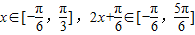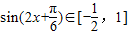∴．…（7分）
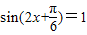当a＞0时，当时，函数的最大值为a²+3a＞10，解得：a＞2（a＜-5舍去）．…（9分）
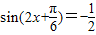当a＜0时，当时，函数的最大值为a²＞10，解得：a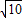＜-（a＞舍去）． …（11分）
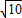综上所述，a 的范围是：a＜-或a＞2，即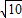（-∞，-）∪（2，+∞）．…（12分）
点评：本题主要考查三角函数的恒等变换，三角函数的最值及其周期性，体现了分类讨论的数学思想，属于中档题．