
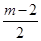 ≥0,即m≥2,所以2≤m≤6时,符合条件.
≥0,即m≥2,所以2≤m≤6时,符合条件.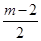 <0,要使|G(x)|在[-1,0]上是减函数,则
<0,要使|G(x)|在[-1,0]上是减函数,则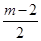 ≤-1且G(0)≤0,所以m≤0;
≤-1且G(0)≤0,所以m≤0;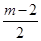 >2,要使|G(x)|在[-1,0]上是减函数,则G(0)≥0,所以m>6.
>2,要使|G(x)|在[-1,0]上是减函数,则G(0)≥0,所以m>6.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 -ax2,a∈R.
-ax2,a∈R.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
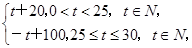 且该商品的日销售量Q与时间t(天)的函数关系为Q=-t+40(0<t≤30,t∈N),则这种商品日销量金额最大的一天是30天中的第________天.
且该商品的日销售量Q与时间t(天)的函数关系为Q=-t+40(0<t≤30,t∈N),则这种商品日销量金额最大的一天是30天中的第________天.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
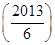 =________.
=________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,若
,若 都是某一三角形的三边长,则称
都是某一三角形的三边长,则称 为“可构造三角形函数”.以下说法正确的是( )
为“可构造三角形函数”.以下说法正确的是( )A. 不是“可构造三角形函数”; 不是“可构造三角形函数”; |
| B.“可构造三角形函数”一定是单调函数; |
C. 是“可构造三角形函数”; 是“可构造三角形函数”; |
D.若定义在 上的函数 上的函数 的值域是 的值域是 ( ( 为自然对数的底数),则 为自然对数的底数),则 一定是“可构造三角形函数”. 一定是“可构造三角形函数”. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com