【题目】已知函数
，则函数
的图象为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
写出分段函数，分段求导后利用导函数的符号或导函数的零点判断函数f（x）的图象的形状．
=
，
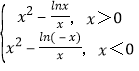当x＜0时，
=
．
令g（x）=2x3﹣1+ln（﹣x），
由
，得
，
当x∈（﹣∞，
）时，g′（x）＞0，当x∈（，0）时，g′（x）＜0．
所以g（x）有极大值为
=
．
又x2＞0，所以f′（x）的极大值小于0．
所以函数f（x）在（﹣∞，0）上为减函数．
当x＞0时，
=
．
令h（x）=2x3﹣1+lnx，
．
所以h（x）在（0，+∞）上为增函数，而h（1）=1＞0，h（
）=﹣
．
又x2＞0，所以函数f′（x）在（0，+∞）上有一个零点，则原函数有一个极值点．
综上函数f（x）的图象为D中的形状．
故选：D．
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】太极图是以黑白两个鱼形纹组成的圆形图案，俗称阴阳鱼，它形象化的表达了阴阳轮转，相反相成是万物生成变化根源的哲理，展现了一种相互转化，相对统一的形式美.如图，按照太极图的构图方法，在平面直角坐标系中，圆
被函数
的图象分割为两个对称的鱼形图案，其中两个小圆的周长均为
，现在大圆内随机取一点，则此点取自阴影部分的概率为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某大型水果超市每天以
元/千克的价格从水果基地购进若干
水果，然后以
元/千克的价格出售，若有剩余，则将剩下的水果以
元/千克的价格退回水果基地，为了确定进货数量，该超市记录了水果最近
天的日需求量（单位：千克），整理得下表：
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以天记录的各日需求量的频率代替各日需求量的概率.
（1）求该超市水果日需求量
（单位：千克）的分布列；
（2）若该超市一天购进水果
千克，记超市当天水果获得的利润为
（单位：元），求的分布列及其数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下几个命题中：
①线性回归直线方程
恒过样本中心
；
②用相关指数
可以刻画回归的效果，值越小说明模型的拟合效果越好；
③随机误差是引起预报值
和真实值
之间存在误差的原因之一，其大小取决于随机误差的方差；
④在含有一个解释变量的线性模型中，相关指数等于相关系数
的平方.
其中真命题的个数为（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】西北某省会城市计划新修一座城市运动公园，设计平面如图所示：其为五边形
，其中三角形区域
为球类活动场所；四边形
为文艺活动场所，
，为运动小道（不考虑宽度）
，
，
千米.
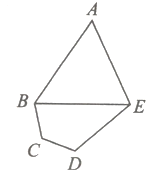
（1）求小道
的长度；
（2）求球类活动场所
的面积最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设A、B、C、D为空间四个不共面的点，以
的概率在每对点之间连一条边，任意两对点之间是否连边是相互独立的，则点A与B可用（一条边或者若干条边组成的）空间折线连接的概率为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
