
【题目】已知函数![]() 的图像与
的图像与![]() 轴相切,
轴相切,![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)求出![]() 的导数,设
的导数,设![]() 的图象与x轴相交于点
的图象与x轴相交于点![]() ,可得
,可得 ,解方程可得
,解方程可得![]() ,原不等式等价于
,原不等式等价于![]() ,设
,设![]() ,求出导数和单调区间,可得极值、最值,即可得证;
,求出导数和单调区间,可得极值、最值,即可得证;
(2)设![]() ,求出导数,运用(1)的结论可得
,求出导数,运用(1)的结论可得![]() 单调递增,再由不等式的性质可得
单调递增,再由不等式的性质可得![]() ,即
,即![]() ,再运用
,再运用![]() 的单调性和不等式的性质,证得
的单调性和不等式的性质,证得![]() ,进而证得右边不等式.
,进而证得右边不等式.
(1)由题得![]() ,设
,设![]() 的图像与
的图像与![]() 轴相切于点
轴相切于点![]() ,则
,则
 ,即
,即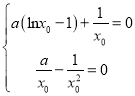 ,解得
,解得![]() ,
,
所以![]() ,则
,则![]() ,即为
,即为![]() .
.
设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() ,即
,即![]() ,
,
所以![]() ;
;
(2)先证![]() ,设
,设![]() ,则
,则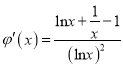 ,
,
由(1)可知,当![]() 时,
时,![]() ,从而有
,从而有![]() ,所以
,所以![]() 单调递增.
单调递增.
又![]() ,从而有
,从而有![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() .
.
再证![]() ,因为
,因为![]()
![]() ,
,
又由(1)知,![]() ,故
,故![]() 在
在![]() 单调递增,
单调递增,
则![]() ,即
,即![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
综上可知,![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC.该曲线段是函数![]() 时的图象,且图象的最高点为B
时的图象,且图象的最高点为B![]() 赛道的中间部分为长
赛道的中间部分为长![]() 千米的直线跑道CD,且CD∥EF;赛道的后一部分是以
千米的直线跑道CD,且CD∥EF;赛道的后一部分是以![]() 为圆心的一段圆弧DE.
为圆心的一段圆弧DE.

(1)求![]() 的值和∠DOE的大小;
的值和∠DOE的大小;
(2)若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路EF上,一个顶点在半径OD上,另外一个顶点P在圆弧DE上,求“矩形草坪”面积的最大值,并求此时P点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若函数f(x)在![]() 处有极值,求函数f(x)的最大值;
处有极值,求函数f(x)的最大值;
(2)是否存在实数b,使得关于x的不等式![]() 在
在![]() 上恒成立?若存在,求出b的取值范围;若不存在,说明理由;
上恒成立?若存在,求出b的取值范围;若不存在,说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再将图像上所有点的横坐标伸长到原来的
个单位长度,再将图像上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图像.
的图像.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果![]() 项有穷数列
项有穷数列![]() 满足
满足![]() ,即
,即![]() ,那么称有穷数列
,那么称有穷数列![]() 为“对称数列”.例如,由组合数组成的数列
为“对称数列”.例如,由组合数组成的数列![]() 就是“对称数列”.
就是“对称数列”.
(1)设数列![]() 是项数为7的“对称数列”,其中
是项数为7的“对称数列”,其中![]() 成等比数列,且
成等比数列,且![]() 写出数列
写出数列![]() 的每一项;
的每一项;
(2)设数列![]() 是项数为
是项数为![]() 的“对称数列”,其中
的“对称数列”,其中![]() 是公差为2的等差数列,且
是公差为2的等差数列,且![]() 求
求![]() 取得最大值时
取得最大值时![]() 的取值,并求最大值;
的取值,并求最大值;
(3)设数列![]() 是项数为
是项数为![]() 的对称数列”,且满足
的对称数列”,且满足![]() 记
记![]() 为数列
为数列![]() 的前
的前![]() 项和,若
项和,若![]() 求
求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在![]() 与正实数
与正实数![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 在
在![]() 处存在距离为
处存在距离为![]() 的对称点,把具有这一性质的函数
的对称点,把具有这一性质的函数![]() 称之为“
称之为“![]() 型函数”.
型函数”.
(1)设![]() ,试问
,试问![]() 是否是“
是否是“![]() 型函数”?若是,求出实数
型函数”?若是,求出实数![]() 的值;若不是,请说明理由;
的值;若不是,请说明理由;
(2)设![]() 对于任意
对于任意![]() 都是“
都是“![]() 型函数”,求实数
型函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,且点
,且点![]() (
(![]() )在直线
)在直线![]() 上.
上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对任意的![]() ,将数列
,将数列![]() 落入区间
落入区间![]() 内的项的个数记为
内的项的个数记为![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)对于(2)中![]() ,记
,记![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() ,求使等式
,求使等式![]() 成立的所有正整数
成立的所有正整数![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《流浪地球》是由刘慈欣的科幻小说改编的电影,在2019年春节档上影,该片上影标志着中国电影科幻元年的到来;为了振救地球,延续百代子孙生存的希望,无数的人前仆后继,奋不顾身的精神激荡人心,催人奋进.某网络调查机构调查了大量观众的评分,得到如下统计表:
评分 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频率 | 0.03 | 0.02 | 0.02 | 0.03 | 0.04 | 0.05 | 0.08 | 0.15 | 0.21 | 0.36 |
(1)求观众评分的平均数?
(2)视频率为概率,若在评分大于等于8分的观众中随机地抽取1人,他的评分恰好是10分的概率是多少?
(3)视频率为概率,在评分大于等于8分的观众中随机地抽取4人,用![]() 表示评分为10分的人数,求
表示评分为10分的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com