
【题目】如图所示,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
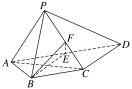
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
【答案】 (1) 证明见解析
(2) 证明见解析
【解析】
(1)连接CE,OF,易知四边形ABCE是菱形,可得O是AC的中点,利用中位线的概念,可得PA∥OF,从而可证AP∥平面BEF;
(2)通过证明AP⊥BE、BE⊥AC,可证明BE⊥平面PAC
证明: (1)如图所示,设AC∩BE=O,连接OF,EC.
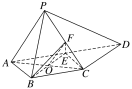
由于E为AD的中点,AB=BC=![]() AD,AD∥BC,
AD,AD∥BC,
所以AE∥BC,且AE=AB=BC,因此,四边形ABCE为菱形,
所以O为AC的中点.又F为PC的中点,
所以在△PAC中,可得AP∥OF.
又OF![]() 平面BEF,AP
平面BEF,AP![]() 平面BEF,
平面BEF,
所以AP∥平面BEF.
(2)由题意,知ED∥BC,ED=BC,
所以四边形BCDE为平行四边形,所以BE∥CD.
又AP⊥平面PCD,所以AP⊥CD,所以AP⊥BE.
因为四边形ABCE为菱形,所以BE⊥AC.
又AP∩AC=A,AP,AC![]() 平面PAC,
平面PAC,
所以BE⊥平面PAC


科目:高中数学 来源: 题型:
【题目】为推行“新课堂”教学法,某老师在甲乙两个班分别用传统教学和“新课堂”两种不同的教学方式进行教学实验.为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图(如下图所示),记成绩不低于70分者为“成绩优良”.

(1)分别计算甲乙两班20个样本中,分数前十的平均分,并据此判断哪种教学方式的教学效果更佳;
(2)甲乙两班40个样本中,成绩在60分以下的学生中任意选取2人,求这2人来自不同班级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=![]() a(0<
a(0<![]() ≦1). w.w.w..c.o.m
≦1). w.w.w..c.o.m
(Ⅰ)求证:对任意的![]()
![]() (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C![]() (t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y=-2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 的零点的个数并说明理由;
的零点的个数并说明理由;
(2)求函数![]() 零点所在的一个区间,使这个区间的长度不超过
零点所在的一个区间,使这个区间的长度不超过![]() ;
;
(3)若![]() ,对于任意的
,对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华传统文化,学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查,小明同学阅读两类读物的阅读量统计如下:
小明阅读“经典名著”的阅读量![]() (单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
(单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
t | 0 | 10 | 20 | 30 |
| 0 | 2700 | 5200 | 7500 |
阅读“古诗词”的阅读量![]() (单位:字)与时间t(单位:分钟)满足如图1所示的关系.
(单位:字)与时间t(单位:分钟)满足如图1所示的关系.

(1)请分别写出函数![]() 和
和![]() 的解析式;
的解析式;
(2)在每天的一小时课外阅读活动中,小明如何分配“经典名著”和“古诗词”的阅读时间,使每天的阅读量最大,最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com