
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
![]() Ⅰ
Ⅰ![]() 求实数a的值;
求实数a的值;
![]() Ⅱ
Ⅱ![]() 若关于x的方程
若关于x的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数b的取值范围;
上恰有两个不相等的实数根,求实数b的取值范围;
![]() Ⅲ
Ⅲ![]() 证明:
证明:![]() 参考数据:
参考数据:![]() .
.
【答案】(1)0;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)求导,由f′(1)=0构造方程求出a;(2)由(1)将方程f(x)+2x=x2+b化简,令g(x)=x2-3x+lnx+b(x>0),求导,研究当x变化时,g′(x),g(x)的变化情况,确定函数的最值,从而建立不等式组,即可求得结论;(3)设φ(x)=lnx-![]() (x2-1),求导,根据函数的单调性得当x≥2时,
(x2-1),求导,根据函数的单调性得当x≥2时,![]() >2
>2![]() ,从而累加可得结论.
,从而累加可得结论.
(1)f′(x)=1-![]() ,∵x=1是f(x)的一个极值点,∴f′(1)=0,即1-
,∵x=1是f(x)的一个极值点,∴f′(1)=0,即1-![]() =0,∴a=0.
=0,∴a=0.
经检验满足题意.
(2)由(1)得f(x)=x-lnx,∴f(x)+2x=x2+b即x-lnx+2x=x2+b,∴x2-3x+lnx+b=0,
设g(x)=x2-3x+lnx+b(x>0),
则g′(x)=2x-3+![]() =
=![]()
=![]() .
.
由g′(x)>0得0<x<![]() 或x>1,由g′(x)<0得
或x>1,由g′(x)<0得![]() <x<1,
<x<1,
∴当x∈![]() ,(1,+∞)时,函数g(x)单调递增,x∈
,(1,+∞)时,函数g(x)单调递增,x∈![]() 时,函数g(x)单调递减,
时,函数g(x)单调递减,
当x=1时,g(x)极小值=g(1)=b-2,g![]() =b-
=b-![]() -ln2,g(2)=b-2+ln2,
-ln2,g(2)=b-2+ln2,
∵方程f(x)+2x=x2+b在![]() 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
∴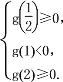 即
即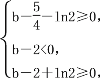 解得
解得![]() +ln2≤b<2.
+ln2≤b<2.
(3)证明:∵k-f(k)=lnk,∴![]()
![]() >
>![]() .
.
![]() +
+![]() +
+![]() +…+
+…+![]() >
>![]() (n∈N,n≥2)
(n∈N,n≥2)
设φ(x)=lnx-![]() (x2-1),则φ′(x)=
(x2-1),则φ′(x)=![]() -
-![]() =
=![]() =-
=-![]()
当x≥2时,φ′(x)<0,∴函数y=φ(x)在[2,+∞)上是减函数,
∴φ(x)≤φ(2)=ln2-![]() <0,∴lnx<
<0,∴lnx<![]() (x2-1).
(x2-1).
∴当x≥2时,![]() >
>![]() =
=![]()
=2![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() >2
>2![]()
=2![]() =
=![]() .
.
∴原不等式成立.


科目:高中数学 来源: 题型:
【题目】某地区上年度电价为0.8元![]() ,年用电量为
,年用电量为![]() ,本年度计划将电价降到0.55 元
,本年度计划将电价降到0.55 元![]() 至0.75元
至0.75元![]() 之间,而用户期待电价为0.4元
之间,而用户期待电价为0.4元![]() ,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元
,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元![]() .(注:收益=实际用电量
.(注:收益=实际用电量![]() (实际电价-成本价)),示例:若实际电价为0.6元
(实际电价-成本价)),示例:若实际电价为0.6元![]() ,则下调电价后新增加的用电量为
,则下调电价后新增加的用电量为![]() 元
元![]() )
)
(1)写出本年度电价下调后,电力部门的收益![]() 与实际电价
与实际电价![]() 的函数关系;
的函数关系;
(2)设![]() ,当电价最低为多少仍可保证电力部门的收益比上一年至少增长
,当电价最低为多少仍可保证电力部门的收益比上一年至少增长![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
(3)是否存在非负实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

表1:设备改造后样本的频数分布表

(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;

(2)根据图3和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价240元;质量指标值落在
内的定为一等品,每件售价240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①A=![]() 的子集有
的子集有![]() 个;
个;
②命题“![]() ”的否定是“
”的否定是“![]() 使得
使得![]() ”;
”;
③“![]() ”是“函数
”是“函数![]() 取得最大值”的充分不必要条件;
取得最大值”的充分不必要条件;
④根据对数定义,对数式![]() 化为指数式
化为指数式![]() ;
;
⑤若![]() ,则
,则![]() 的取值范围为
的取值范围为![]() ;
;
⑥![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,试探究:直线
,试探究:直线![]() 是否过定点,若是,求该定点的坐标,若不是,请说明.
是否过定点,若是,求该定点的坐标,若不是,请说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com