
【题目】如图,在三棱椎![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,过线段
的中点,过线段![]() 的中点
的中点![]() 作
作![]() 的平行线,分别交
的平行线,分别交![]() 于点
于点![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明略;(2)![]() .
.
【解析】
试题(1)要证线面垂直,就要证线线垂直,即要证![]() 与平面
与平面![]() 内两条相交直线垂直,首先由三棱柱侧棱与底面垂直可得
内两条相交直线垂直,首先由三棱柱侧棱与底面垂直可得![]() ,由等腰三角形性质知
,由等腰三角形性质知![]() ,从而有
,从而有![]() ,因此即证线面垂直;(2)要求二面角,关键是作出二面角的平面角,一般要找到二面角的一个面的垂线,则平面角易作,因此我们连接
,因此即证线面垂直;(2)要求二面角,关键是作出二面角的平面角,一般要找到二面角的一个面的垂线,则平面角易作,因此我们连接![]() ,作
,作![]() 于
于![]() ,由(1)可证
,由(1)可证![]() 平面
平面![]() ,根据三垂线定理可得所求二面角的平面角,并在相应直角三角形中可求得此角大小.
,根据三垂线定理可得所求二面角的平面角,并在相应直角三角形中可求得此角大小.
试题解析:(1)因为AB=AC,D是BC的中点,
所以BC⊥AD.
由题可知MN∥BC,
所以MN⊥AD.
因为AA1⊥平面ABC,MN平面ABC,
所以AA1⊥MN.
又AD,AA1在平面ADD1A1内,且AD与AA1相交于点A,
所以MN⊥平面ADD1A1.
(2)解 如图,连结A1P,过点A作AE⊥A1P于点E,过点E作EF⊥A1M于点F,连结AF.
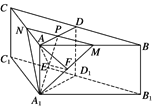
由(1)知,MN⊥平面AEA1,
所以平面AEA1⊥平面A1MN.
因为平面AEA1∩平面A1MN=A1P,AE⊥A1P,AE平面AEA1,
所以AE⊥平面A1MN,则A1M⊥AE,又AE∩EF=E,
所以A1M⊥平面AEF,则A1M⊥AF,
故∠AFE为二面角A-A1M-N的平面角(设为θ).
设AA1=1,则由AB=AC=2AA1,∠BAC=120°,
D为BC的中点,有∠BAD=60°,AB=2,AD=1.
又P为AD的中点,M为AB的中点,
所以AP=![]() ,AM=1.
,AM=1.
在Rt△AA1P中,A1P=![]() ,
,
在Rt△A1AM中,A1M=![]() ,
,
从而AE=![]() ,
,
AF=![]() ,
,
所以sinθ=![]() .
.
因为∠AFE为锐角,
所以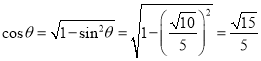 .
.
故二面角A-A1M-N的余弦值为![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的各条棱长均相等,
的各条棱长均相等, ![]() 为
为![]() 的中点,
的中点, ![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )
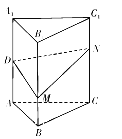
A. 平面![]() 平面
平面![]() B. 三棱锥
B. 三棱锥![]() 的体积为定值
的体积为定值
C. ![]() 可能为直角三角形 D. 平面
可能为直角三角形 D. 平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 也为抛物线
也为抛物线![]() 的焦点,点
的焦点,点![]() 为
为![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)延长![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,求三角形
,求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.


图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学专著《九章算术》中有一个“两鼠穿墙题”,其内容为:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半.问何日相逢?各穿几何?”如图的程序框图源于这个题目,执行该程序框图,若输入x=20,则输出的结果为( )
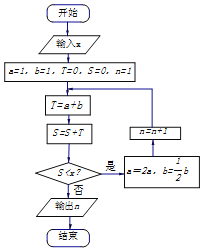
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(2,
(φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(2,![]() ),半径为1的圆.
),半径为1的圆.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)设M为曲线C1上的点,N为曲线C2上的点,求|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 交于
交于![]() 不同两点分别过点
不同两点分别过点![]() 、点
、点![]() 作抛物线
作抛物线![]() 的切线,所得的两条切线相交于点
的切线,所得的两条切线相交于点![]() .
.
(Ⅰ)求证![]() 为定值:
为定值:
(Ⅱ)求![]() 的面积的最小值及此时的直线
的面积的最小值及此时的直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
运动达人 | 参与者 | 合计 | |
男教师 | 60 | 20 | 80 |
女教师 | 40 | 20 | 60 |
合计 | 100 | 40 | 140 |
(1)根据上表说明,能否在犯错误概率不超过0.05的前提下认为获得“运动达人”称号与性别有关?
(2)从具有“运动达人”称号的教师中,采用按性别分层抽样的方法选取10人参加全国第四届“万步有约”全国健走激励大赛某赛区的活动,若从选取的10人中随机抽取3人作为代表参加开幕式,设抽取的3人中女教师人数为![]() ,写出
,写出![]() 的分布列并求出数学期望
的分布列并求出数学期望![]() .
.
参考公式: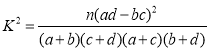 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com