
分析 求点B到面GEF的距离,就是求C到平面EFG距离的 $\frac{1}{3}$,直接作垂线求解即可.
解答 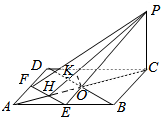 解:如图,连接EP、FP、EF、BD、AC、EF、BD分别交AC于H、O.因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
解:如图,连接EP、FP、EF、BD、AC、EF、BD分别交AC于H、O.因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
BD不在平面EFP上.否则,平面EFP和平面ABCD重合,从而点P在平面的ABCD上,与题设矛盾.
由直线和平面平行的判定定理知BD∥平面EFP,所以BD和平面EFP的距离就是点B到平面EFP的距离.
∵BD⊥AC,
∴EF⊥HC.
∵PC⊥平面ABCD,
∴EF⊥PC,
∴EF⊥平面HCP.
∴平面EFP⊥平面HCP,HP是这两个垂直平面的交线.
作OK⊥HP交HP于点K,由两平面垂直的性质定理知OK⊥平面EFP,所以线段OK的长就是点B到平面EFP的距离.
∵正方形ABCD的边长为4,PC=2,
∴AC=4$\sqrt{2}$,HO=$\sqrt{2}$,HC=3$\sqrt{2}$.
∴在Rt△HCP中,HP=$\sqrt{{(3\sqrt{2})}^{2}+{2}^{2}}$=$\sqrt{22}$.
由于Rt△HKO和Rt△HCP有一个锐角是公共的,故Rt△HKO∽△HCP.
∴OK=$\frac{HO•PC}{PH}$=$\frac{2×\sqrt{2}}{\sqrt{22}}$=$\frac{2\sqrt{11}}{11}$.
即点B到平面EFP的距离为$\frac{2\sqrt{11}}{11}$.
点评 本题主要考查直线与平面的位置关系、平面与平面的位置关系、点到平面的距离等有关知识,考查学生的空间想象能力和思维能力,属于中档题.解决此类问题应该注意从三维空间向二维平面的转化,从而找到解题的捷径.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°AB=AC=2,AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
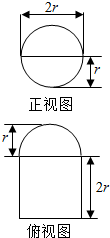 圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.
圆柱被一个平面截去一部分与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若半球的半径r=2,则该几何体的表面积为16+20π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com