
某校高一学生1000人,每周一次同时在两个可容纳600人的会议室,开设“音乐欣赏”与“美术鉴赏”的校本课程.要求每个学生都参加,要求第一次听“音乐欣赏”课的人数为
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第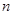 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
(1)若 ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
;
(2)①证明数列 是等比数列,并用
是等比数列,并用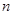 表示
表示 ;
;
②若要求前十次参加“音乐欣赏”课的学生的总人次不超过5800,求 的取值范围.
的取值范围.
(1)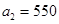 ,
,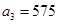 (2)①
(2)①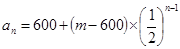 ②
②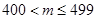 ,且
,且
解析试题分析:解决数列实际应用问题的关键是把实际问题随着正整数变化的量用数列表达出来,然后利用数列知识对表达的数列进行求解(求和、研究单调性、最值等),根据求解结果对实际问题作出答案.根据题意(1) ,分别取
,分别取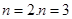 ,即可求出
,即可求出 ,(2)①由题意得
,(2)①由题意得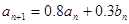 ,由
,由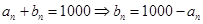 ,代入
,代入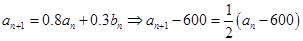 即可得证;②前十次听“音乐欣赏”课的学生总人次即为数列
即可得证;②前十次听“音乐欣赏”课的学生总人次即为数列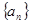 的前10项和
的前10项和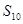 ,根据题意,
,根据题意,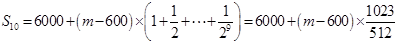 ,由已知,
,由已知,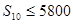 ,得
,得 ,解之即可.
,解之即可.
(1)由已知 ,又
,又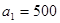 ,
,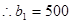 ,
,
∴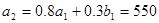 ,
,
∴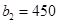 ,
,
∴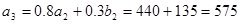 .
.
(2) ①由题意得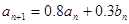 ,
,
∴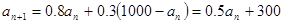 ,
,
∴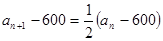 ,
, 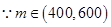 ,∴
,∴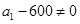 ,
,
∴数列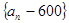 是等比数列,公比为
是等比数列,公比为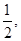 首项为
首项为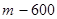
∴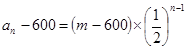 ,
,
得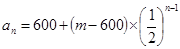
②前十次听“音乐欣赏”课的学生总人次即为数列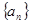 的前10项和
的前10项和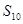 ,
,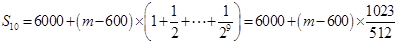 ,
,
由已知,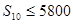 ,得
,得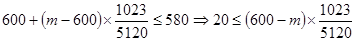 ,
,
∴ ,∴
,∴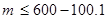 ,
,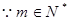 ,∴
,∴ 的取值范围是
的取值范围是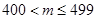 ,且
,且 .
.
考点:数列的实际应用问题


科目:高中数学 来源: 题型:解答题
某企业为加大对新产品的推销力度,决定从今年起每年投入100万元进行广告宣传,以增加新产品的销售收入.已知今年的销售收入为250万元,经市场调查,预测第n年与第n-1年销售收入an与an-1(单位:万元)满足关系式:an=an-1+ -100.
-100.
(1)设今年为第1年,求第n年的销售收入an;
(2)依上述预测,该企业前几年的销售收入总和Sn最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利a元的前提下,可卖出b件;若做广告宣传,广告费为n千元比广告费为 千元时多卖出
千元时多卖出 件。
件。
(1)试写出销售量 与n的函数关系式;
与n的函数关系式;
(2)当 时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
时,厂家应该生产多少件产品,做几千元的广告,才能获利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com