练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某大学志愿者协会有6名男同学，4名女同学，在这10名同学中，3名同学来自数学学院，其余7名同学来自物理﹑化学等其他互不相同的七个学院，现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）.

    (1)求选出的3名同学是来自互不相同学院的概率；

    (2)设为选出的3名同学中女同学的人数，求随机变量的分布列.

    【答案】（1）（2）详见解析

    【解析】

    （1）利用排列组合求出所有基本事件个数及选出的3名同学是来自互不相同学院的基本事件个数，代入古典概型概率公式求出即可（2）随机变量X的所有可能值为0,1,2,3，，列出随机变量X的分布列即可.

    （1）设“选出的3名同学是来自互不相同的学院”为事件，

    则

    （2）随机变量的所有可能值为

    的分布列为

    X

    0

    1

    2

    3

    P

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，判断在的单调性，并用定义证明．

    （2）若对任意，不等式恒成立，求的取值范围；

    （3）讨论零点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线过，倾斜角为，以为极点， 轴在平面直角坐标系中，直线，曲线（为参数），坐标原点为极点，以轴正半轴为极轴，建立极坐标系.

    （1）求的极坐标方程；

    （2）若曲线的极坐标方程为，且曲线分别交于点两点，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）求函数的单调区间；

    （Ⅱ）若对定义域每的任意恒成立，求实数的取值范围；

    （Ⅲ）证明：对于任意正整数，不等式恒成立。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4:坐标系与参数方程

    在平面直角坐标系xoy中,已知直线的参数方程为为参数, 以原点O为极点,以轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为

    (1)写出直线的极坐标方程和曲线C的直角坐标方程;

    (2)若直线与曲线C相交于A,B 两点,求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 为向国际化大都市目标迈进，沈阳市今年新建三大类重点工程，它们分别是30项基础设施类工程，20项民生类工程和10项产业建设类工程.现有来沈阳的3名工人相互独立地从这60个项目中任选一个项目参与建设.

    （Ⅰ）求这3人选择的项目所属类别互异的概率；

    （Ⅱ）将此3人中选择的项目属于基础设施类工程或产业建设类工程的人数记为，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.

    （1）求抛物线方程;

    （2）直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

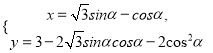    在直角坐标系中，曲线的参数方程为（为参数）．以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线的极坐标方程为．　

    （1）当时，求曲线和曲线的交点的直角坐标；

    （2）当时，设， 分别是曲线与曲线上动点，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，四边形是等腰梯形， ， ， 平面， ， .

    （1）求证： ；

    （2）求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案