
分析 (1)h(x)=y=$\frac{f(x)}{g(x)}$=$\frac{lnx}{x}$(x>0).h′(x)=$\frac{1-lnx}{{x}^{2}}$,令h′(x)=0,解得x=e.利用导数研究函数的单调性极值与最值即可得出函数y=$\frac{f(x)}{g(x)}$的最大值为h(e).
(2)x>1,f(x)>2g($\frac{x-1}{x+1}$)?x>1时,lnx>2$\frac{x-1}{x+1}$?(x+1)lnx-2(x-1)>0,x>1.令u(x)=(x+1)lnx-2(x-1)>0,x>1,u(1)=0.利用导数研究函数的单调性极值最值即可得出.
解答 (1)解:h(x)=y=$\frac{f(x)}{g(x)}$=$\frac{lnx}{x}$(x>0).
h′(x)=$\frac{1-lnx}{{x}^{2}}$,令h′(x)=0,解得x=e.
可知:x>e时,h′(x)<0,此时函数h(x)单调递减;0<x<e时,h′(x)>0,此时函数h(x)单调递增.
∴x=e时,函数h(x)取得极小值即最大值.
∴函数y=$\frac{f(x)}{g(x)}$的最大值为h(e)=$\frac{1}{e}$.
(2)证明:x>1,f(x)>2g($\frac{x-1}{x+1}$)?x>1时,lnx>2$\frac{x-1}{x+1}$?(x+1)lnx-2(x-1)>0,x>1.
令u(x)=(x+1)lnx-2(x-1)>0,x>1,u(1)=0.
u′(x)=lnx+$\frac{x+1}{x}$-2=$\frac{xlnx+1-x}{x}$.
令v(x)=xlnx+1-x,x>1.
v′(x)=lnx>ln1=0.
∴函数v(x)在x>1时单调递增,∴v(x)>v(1)=0.
∴u′(x)>0,
∴函数u(x)在x>1时单调递增,u(x)>u(1)=0.
∴(x+1)lnx-2(x-1)>0,x>1.即x>1,f(x)>2g($\frac{x-1}{x+1}$).
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
若x,y满足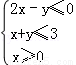 ,则目标函数z=2x+y的最大值为( )
,则目标函数z=2x+y的最大值为( )
A.0 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位长度:cm),则此几何体的侧面积是( )
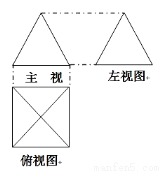
A.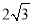 cm
cm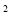 B.
B.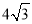 cm2
cm2
C.8 cm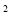 D.14 cm2
D.14 cm2
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com