
| A. | $\frac{17}{9}$ | B. | $\frac{19}{10}$ | C. | $\frac{9}{5}$ | D. | $\frac{11}{6}$ |
分析 观察下列各式,右边分母组成以3为首项,1为公差的等差数列;分子组成以4为首项,2为公差的等差数列,即可得出结论.
解答 解:1+$\frac{1}{1+2}$=$\frac{4}{3}$,1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$=$\frac{3}{2}$=$\frac{6}{4}$,1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+$\frac{1}{1+2+3+4}$=$\frac{8}{5}$,…,
∴1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+…+9}$=$\frac{18}{10}$=$\frac{9}{5}$.
故选:C.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:选择题
| A. | 0对 | B. | 1对 | C. | 2对 | D. | 3对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
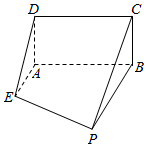 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (0,1) | C. | [2,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -8 | C. | -2 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com