
����Ŀ���������ҿ�ݹ�˾�䡰���С�硱���չ��ʷ������£���˾�涨��н![]() Ԫ��ÿ�����
Ԫ��ÿ�����![]() Ԫ���ҹ�˾�涨��н
Ԫ���ҹ�˾�涨��н![]() Ԫ��ÿ��ǰ
Ԫ��ÿ��ǰ![]() ����ɣ�����
����ɣ�����![]() ���IJ���ÿ�����
���IJ���ÿ�����![]() Ԫ
Ԫ
��1������ҿ�ݹ�˾�ġ����С�硱һ�չ���![]() ����λ��Ԫ�����ͻ�����
����λ��Ԫ�����ͻ�����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() ����
����![]() ��
��
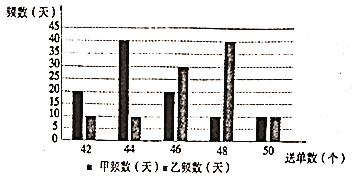
��2������ͬһ��˾�ġ����С�硱һ���ͻ�������ͬ���ִ����ҹ�˾�������ȡһ�������С�硱������¼��![]() ����ͻ��������õ���������ͼ:
����ͻ��������õ���������ͼ:
����Ƶ����Ϊ���ʣ��ش��������⣺
�ټ��ҿ�ݹ�˾�ġ����С�硱�չ���Ϊ![]() ����λ��Ԫ������
����λ��Ԫ������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��С������ҹ�˾�е�һ��ӦƸ�����С�硱�Ĺ������������������ĽǶȿ��ǣ�����������ѧ��ͳ��ѧ֪ʶΪ������ѡ��˵������.
���𰸡���1���ף� ![]() ���ң�
���ң� 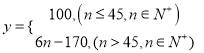 ��2���ټ��������Ƽ�С��ȥ�ҿ�ݹ�ʽӦƸ.
��2���ټ��������Ƽ�С��ȥ�ҿ�ݹ�ʽӦƸ.
�������������������1���ɷֶκ�����д�������С���ͻ������빤�ʵĺ�����ϵʽ����2����������ͳ��ͼ�ɵ�![]() �Ŀ���ȡֵ��Χ��������Ӧ�ĸ���ֵ���ɵ÷ֲ��У���һ���������ѧ�������ڿ���������ݹ�˾�Ŀ��С�����ƽ�����ʣ��Ƽ�С��ȥƽ�����ʽϸߵĹ�˾�ϰ࣮
�Ŀ���ȡֵ��Χ��������Ӧ�ĸ���ֵ���ɵ÷ֲ��У���һ���������ѧ�������ڿ���������ݹ�˾�Ŀ��С�����ƽ�����ʣ��Ƽ�С��ȥƽ�����ʽϸߵĹ�˾�ϰ࣮
�����������1����ݹ�ʽ�ġ����С�硱һ�չ���![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
![]()
�ҿ�ݹ�ʽ�ġ����С�硱һ�չ���![]() ����λ��Ԫ�����͵���
����λ��Ԫ�����͵���![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
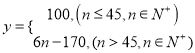 .
.
��2���ټ��ҿ�ݹ�˾�ġ����С�硱�չ���Ϊ![]() ����λ��Ԫ����������ͼ��
����λ��Ԫ����������ͼ��![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ��
��
![]()
![]() ��
��
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��

���ҿ�ݹ�˾�ġ����С�硱��ƽ���͵���Ϊ�� ![]() ��
��
�����ҿ�ݹ�˾�ġ����С�硱��ƽ������Ϊ![]() ��Ԫ����
��Ԫ����
�ɢ�֪����ݹ�˾�ġ����С�硱��ƽ������Ϊ![]() Ԫ.
Ԫ.
���Ƽ�С��ȥ�ҿ�ݹ�ʽӦƸ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����2csinBcosA��bsinC=0��
��1�����A��
��2������ABC�����Ϊ ![]() ��b+c=5����a��
��b+c=5����a��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2��2x��x��[��1��2]����ֵ��Ϊ����A��g��x��=ax+2��x��[��1��2]����ֵ��Ϊ����B����AB����ʵ��a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪij��2017��2��28����տ�������ָ������ͼ.
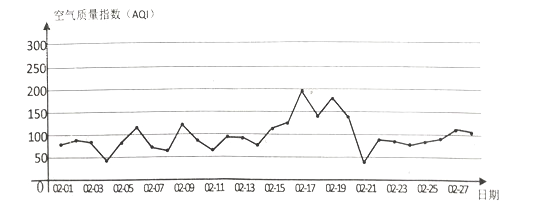
���й�����������������ƽ̨�ṩ�Ŀ�������ָ�������£�

��1�����������������ͼ��ȫ�·���Ƶ�ʷֲ�ֱ��ͼ������Ǧ��Ϳ�ھ����������������2�·ݿ�������ָ��������ݵ�ƽ����������С�����һλ����
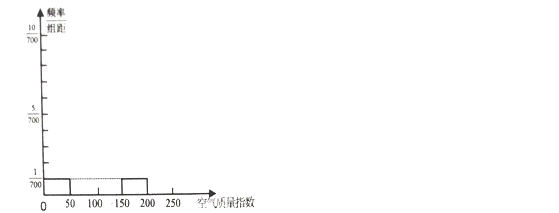
��2���о���Ա���֣���������ָ��������![]() ��ȼ���ŷŵ�
��ȼ���ŷŵ�![]() ������Ŀ����������ع�ϵ����
������Ŀ����������ع�ϵ����![]() Ϊ��λ���±�����
Ϊ��λ���±�����![]() ��
��![]() ��������ݣ�
��������ݣ�

��![]() ����
����![]() �Ļع鷽�̣������Ƶ�
�Ļع鷽�̣������Ƶ�![]() �ŷ�����
�ŷ�����![]() ʱ��
ʱ�� ![]() ��ֵ.
��ֵ.
������С���˷���ع鷽�̵�ϵ����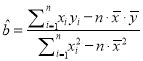 ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��������
��������![]() ���㣺
���㣺![]() ����
����![]() ��
��![]() ��
��![]() ��.
��.
����������![]() ��ͨ�ʽ��
��ͨ�ʽ��
������֤������![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�
����������![]() ��ǰ
��ǰ![]() ��͵���Сֵ.
��͵���Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�溯��f��x������f��x+2��=f��x��2������x�ʣ�0��1��ʱ��f��x��=3x �� ��f�� ![]() ��= ��
��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=|x+1|+|x��1|��
��1����f��x����x+2�Ľ⼯��
��2��������ʽf��x����log2��a2��4a+12��������ʵ��a���������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x�����溯����g��x����ż���������ڹ���������{x|x��R��x�١�1}������f��x��+g��x��= ![]() ��
��
��1����f��x����g��x���Ľ���ʽ��
��2����h��x��=f��x����g��x������h�� ![]() ����
����
��3����ֵ��h��2��+h��3��+h��4��+��+h��2016��+h�� ![]() ��+h��
��+h�� ![]() ��+h��
��+h�� ![]() ��+��+h��
��+��+h�� ![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ����ۣ�
�������� ![]() ����p��x��R��x2+x+1��0��
����p��x��R��x2+x+1��0��
�ڡ���x��3����x��4��=0���ǡ�x��3=0���ij�ֶ�����Ҫ������
�����⡰��m��0����x2+x��m=0��ʵ���������������Ϊ����������x2+x��m=0û��ʵ��������m��0����
����a��0��b��0��a+b=4���� ![]() ����СֵΪ1��
����СֵΪ1��
������ȷ���۵ĸ���Ϊ�� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com