
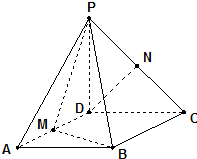
 已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°的菱形且PD=AD=2,又PD⊥底面ABCD,点M、N分别是棱AD、PC的中点.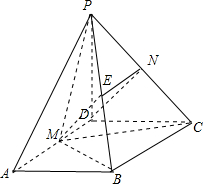 DN∥ME,且ME?平面PMB,DN?平面PMB;
DN∥ME,且ME?平面PMB,DN?平面PMB;| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
| 2 |
| 1 |
| 2 |
| 8-1 |
| 7 |
| 1 |
| 3 |
| 7 |
2
| ||
| 3 |
2
| ||
| 7 |
2
| ||
| 7 |


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
| A、M∪P |
| B、M∩P |
| C、(∁SM)∪(∁SP) |
| D、(∁SM)∩(∁SP) |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| A、k≤-2 |
| B、-2≤k<-1 |
| C、-1<k<0 |
| D、k≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 7 |
| 16 |
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax |
| 9 |
A、(-∞,-
| ||||
B、[-
| ||||
C、[
| ||||
D、(-∞,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、天上无云下大雨 |
| B、同性电荷,相互排斥 |
| C、没有水分,种子发芽 |
| D、从分别标有1,2,3,4,5,6,7,8,9,10的10张号签中任取一张,得到1号签 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com