
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若曲线C的极坐标方程为ρsin2θ+4sinθ﹣ρ=0,直线l: ![]() (t为参数)过曲线C的焦点,且与曲线C交于M,N两点.
(t为参数)过曲线C的焦点,且与曲线C交于M,N两点.
(1)写出曲线C及直线l直角坐标方程;
(2)求|MN|.
【答案】
(1)解:曲线C的极坐标方程为ρsin2θ+4sinθ﹣ρ=0,
可得ρ2sin2θ+4ρsinθ﹣ρ2=0,可得直角坐标方程:y2+4y﹣(x2+y2)=0,即x2=4y.
直线l: ![]() (t为参数)消去参数t可得普通方程:y﹣3=(x﹣2)tanα.
(t为参数)消去参数t可得普通方程:y﹣3=(x﹣2)tanα.
由题意可知:直线经过点(0,1),∴﹣2=﹣2tanα,可得tanα=1.
∴直线l的方程为:y﹣3=x﹣2,化为y=x+1
(2)解:联立 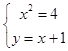 ,化为:x2﹣4x﹣4=0,
,化为:x2﹣4x﹣4=0,
∴|MN|= ![]() =
= ![]() =8
=8
【解析】(1)曲线C的极坐标方程为ρsin2θ+4sinθ﹣ρ=0,可得ρ2sin2θ+4ρsinθ﹣ρ2=0,利用互化公式可得直角坐标方程.由直线l的参数方程,消去参数t可得普通方程,把抛物线焦点(0,1)代入即可得出.(2)直线方程与抛物线方程联立化为:x2﹣4x﹣4=0,利用根与系数的关系及其|MN|= ![]() 即可得出.
即可得出.


科目:高中数学 来源: 题型:
【题目】为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间![]() ,
, ![]() ,
, ![]() ,
, ![]() 进行分组,得到频率分布直方图如图所示,已知样本中体重在区间
进行分组,得到频率分布直方图如图所示,已知样本中体重在区间![]() 上的女生数与体重在区间
上的女生数与体重在区间![]() 上的女生数之比为
上的女生数之比为![]() .
.

(1)求![]() 的值;
的值;
(2)从样本中体重在区间![]() 上的女生中随机抽取两人,求体重在区间
上的女生中随机抽取两人,求体重在区间![]() 上的女生至少有一人被抽中的概率.
上的女生至少有一人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=1,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为  为参数).
为参数).
(1)写出直线l与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 ![]() 得到曲线C′,设曲线C′上任一点为M(x,y),求
得到曲线C′,设曲线C′上任一点为M(x,y),求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是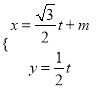 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com