
| A. | $\sqrt{7}\;km$ | B. | $\sqrt{13}\;km$ | C. | $\sqrt{19}\;km$ | D. | $\sqrt{10-3\sqrt{3}}\;km$ |
分析 分别计算出AD,BC.在△ABC中,由余弦定理可得AC;在△ACD中,由余弦定理即可得出DC.
解答 解:如图所示.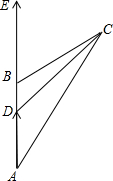 15min=$\frac{1}{4}$h.
15min=$\frac{1}{4}$h.
设甲、乙两船行驶$\frac{1}{4}$h分别到D、C点.
∴AD=$\frac{1}{4}$×8=2km.BC=$\frac{1}{4}$×12=3km.
∵∠EBC=60°,∴∠ABC=120°.
∵AB=BC=3,
∴∠A=∠ACB=30°.
在△ABC中,由余弦定理可得:
AC2=AB2+BC2-2AB•BCcos∠ABC=32+32-2×3×3cos120°=27,
∴AC=3$\sqrt{3}$.
在△ACD中,由余弦定理可得:DC2=AD2+AC2-2AD•ACcos∠DAC
=4+27-2×$2×3\sqrt{3}$cos30°=13.
∴DC=$\sqrt{13}$.
故选:B.
点评 本题考查了利用余弦定理解三角形、行程问题,考查了推理能力和计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 18 | C. | 12 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
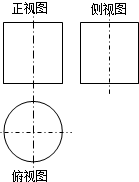 如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{5}{4}π$ | C. | π | D. | $\frac{3}{2}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
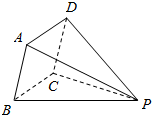 各棱长都为2的四棱锥,底面ABCD是正方形,将侧面PBC水平放置,则这个几何体的俯视图的面积为( )
各棱长都为2的四棱锥,底面ABCD是正方形,将侧面PBC水平放置,则这个几何体的俯视图的面积为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
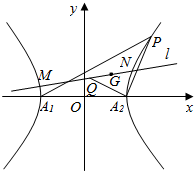 已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.
已知中心在原点,左、右顶点A1、A2在x轴上,离心率为$\frac{\sqrt{21}}{3}$的双曲线C经过点P(6,6),动直线l经过△A1PA2的重心G与双曲线C交于不同两点M、N,Q为线段MN的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com