
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的最大值.
【答案】
(1)解:设 ![]()
则a=2RsinA,b=2RsinB,c=2RsinC
∵2asinA=(2b+c)sinB+(2c+b)sinC
方程两边同乘以2R
∴2a2=(2b+c)b+(2c+b)c
整理得a2=b2+c2+bc
∵由余弦定理得a2=b2+c2﹣2bccosA
故cosA=﹣ ![]() ,A=120°
,A=120°
(2)解:由(1)得:sinB+sinC
=sinB+sin(60°﹣B)
= ![]() cosB+
cosB+ ![]() sinB
sinB
=sin(60°+B)
故当B=30°时,sinB+sinC取得最大值1
【解析】(1)根据正弦定理,设 ![]() ,把sinA,sinB,sinC代入2asinA=(2b+c)sinB+(2c+b)sinC求出a2=b2+c2+bc,再与余弦定理联立方程,可求出cosA的值,进而求出A的值.(2)根据(1)中A的值,可知c=60°﹣B,化简得sin(60°+B)根据三角函数的性质,得出最大值.
,把sinA,sinB,sinC代入2asinA=(2b+c)sinB+(2c+b)sinC求出a2=b2+c2+bc,再与余弦定理联立方程,可求出cosA的值,进而求出A的值.(2)根据(1)中A的值,可知c=60°﹣B,化简得sin(60°+B)根据三角函数的性质,得出最大值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中 ![]() )的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sin2x的图象,则只需将f(x)的图象( ) 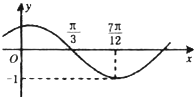
A.向右平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( ) 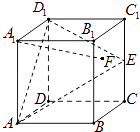
A.{t| ![]() }
}
B.{t| ![]() ≤t≤2}??
≤t≤2}??
C.{t|2 ![]() }
}
D.{t|2 ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 的交点的直角坐标.
的交点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有体育特长生25人,美术特长生35人,音乐特长生40人.用分层抽样的方法从中抽取40人,则抽取的体育特长生、美术特长生、音乐特长生的人数分别为( )
A.8,14,18
B.9,13,18
C.10,14,16
D.9,14,17
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com