
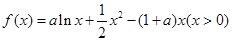 .
.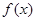 的单调区间;
的单调区间;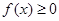 在
在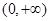 内恒成立,求实数
内恒成立,求实数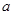 的取值范围.
的取值范围.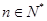 ,求证:
,求证: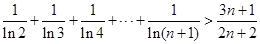 .
. 时,
时,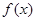 在
在 单调递减,在
单调递减,在 上单调递增;
上单调递增; 时,
时,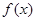 在
在 单调递减,在
单调递减,在 ,
, 上单调递增;
上单调递增; 时,
时,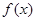 在
在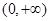 上单调递增;
上单调递增; 时,
时,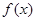 在
在 单调递减, 在
单调递减, 在 ,
,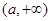 上单调递增;
上单调递增;
 使得
使得 ,则
,则 ;若任意
;若任意 使得
使得 ,则
,则 .由
.由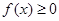 得:
得: 恒成立,所以
恒成立,所以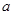 小于等于
小于等于 的最小值.
的最小值. 外,
外, 是
是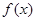 的一个极值点,故可首先考虑
的一个极值点,故可首先考虑 这个特殊值.由
这个特殊值.由 得:
得: 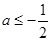 ,这样只需考虑
,这样只需考虑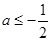 时
时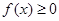 在
在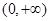 内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度.
内是否恒成立.这是本题的特点,需要仔细观察、分析.若发现其特点,则运算大大简化.所以这个题有较好的区分度. 可得:
可得: ,由此可将不等式左边各项放缩.
,由此可将不等式左边各项放缩.
 时,
时,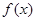 在
在 单调递减,在
单调递减,在 上单调递增;
上单调递增; 时,
时,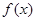 在
在 单调递减,在
单调递减,在 ,
, 上单调递增;
上单调递增; 时,
时,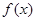 在
在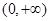 上单调递增;
上单调递增; 时,
时,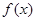 在
在 单调递减, 在
单调递减, 在 ,
,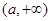 上单调递增.
上单调递增.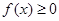 得:
得:
 ,则
,则
 ,则
,则 即
即
 得
得
 在
在 内单调递减,在
内单调递减,在 内单调递增.所以
内单调递增.所以
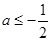
 得:
得: 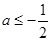
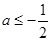 时,
时, 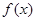 在
在 单调递减,在
单调递减,在 上单调递增
上单调递增
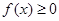 在
在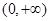 内恒成立,实数
内恒成立,实数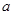 的取值范围为
的取值范围为 .
. 时,
时,  即
即 (
( 时取等号)
时取等号) 时:
时: 
 ,所以
,所以 .
.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:不详 题型:解答题
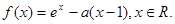
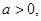 求函数
求函数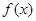 在
在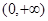 上的极值;
上的极值;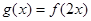 ,设函数
,设函数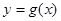 的图像
的图像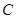 与
与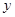 轴交于
轴交于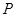 点,曲线
点,曲线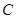 在
在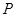 点处的切线与两坐标轴所围成图形的面积为
点处的切线与两坐标轴所围成图形的面积为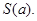 则当
则当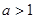 时,求
时,求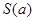 的最小值.
的最小值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
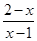 +aln(x-1)(a∈R).
+aln(x-1)(a∈R).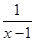 <2ln(x-1)<2x-4(x>2);
<2ln(x-1)<2x-4(x>2);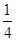 +
+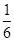 +…+
+…+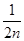 <lnn<1+
<lnn<1+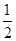 + +
+ +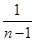 (n∈N*,且n≥2).
(n∈N*,且n≥2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com