
【题目】写出下列命题的否定,并判断真假:
(1)不论![]() 取何实数,方程
取何实数,方程![]() 必有实数根;
必有实数根;
(2)所有末位数字是0或5的整数都能被5整除;
(3)某些梯形的对角线互相平分;
(4)被8整除的数能被4整除.
【答案】(1)存在实数![]() ,使得方程
,使得方程![]() 没有实数根,真命题;(2)存在末位数字是0或5的整数不能被5整除,是假命题;(3)任一个梯形的对角线都不互相平分,是真命题;(4)存在一个数能被8整除,但不能被4整除,是假命题.
没有实数根,真命题;(2)存在末位数字是0或5的整数不能被5整除,是假命题;(3)任一个梯形的对角线都不互相平分,是真命题;(4)存在一个数能被8整除,但不能被4整除,是假命题.
【解析】
(1) 先将命题改写成含全称量词的形式得到全称命题,再将全称命题写成特称命题即可,利用判别式小于零有解说明命题是真命题.
(2) 先将命题改写成含全称量词的形式得到全称命题,再将全称命题写成特称命题即可,显然是假命题.
(3)先将命题改写成含特称量词的形式得到特称命题,再将特称命题写成全称命题即可,是真命题.
(4)先将命题改写成含全称量词的形式得到全称命题,再将全称命题写成特称命题即可,是假命题.
(1)这一命题可以表述为![]() 对所有的实数
对所有的实数![]() ,方程
,方程![]() 都有实数根,其否定是
都有实数根,其否定是![]() 存在实数
存在实数![]() ,使得方程
,使得方程![]() 没有实数根.当
没有实数根.当![]() ,即
,即![]() 时,该方程没有实根,因此
时,该方程没有实根,因此![]() 是真命题.
是真命题.
(2)命题的否定:存在末位数字是0或5的整数不能被5整除,是假命题.
(3)命题的否定:任一个梯形的对角线都不互相平分,是真命题.
(4)命题的否定:存在一个数能被8整除,但不能被4整除,是假命题.


科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴,与坐标系
轴为非负半轴为极轴,与坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求倾斜角
有公共点,求倾斜角![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
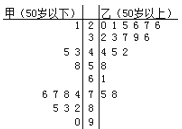
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的图形中,每个三角形上各有一个数字,若六个三角形上的数字之和为![]() ,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为
,则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为![]() ,现从
,现从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( )
中任取两个数字标在另外两个三角形上,则恰好使该图形为“和谐图形”的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com