
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率.
斜率.
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.
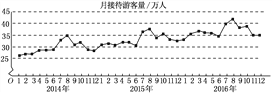
根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边长分别为a,b,c,且cos2B﹣cos2A=2sinC(sinA﹣sinC).
(1)求角B的大小;
(2)若 ![]() ,求2a+c的取值范围.
,求2a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 内一点
内一点![]() ,直线
,直线![]() 过点
过点![]() 且与圆
且与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求圆![]() 的圆心坐标和面积;
的圆心坐标和面积;
(2)若直线![]() 的斜率为
的斜率为![]() ,求弦
,求弦![]() 的长;
的长;
(3)若圆上恰有三点到直线![]() 的距离等于
的距离等于![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的对称轴为坐标轴,顶点是坐标原点,准线方程为![]() ,直线
,直线![]() 与抛物线相交于不同的
与抛物线相交于不同的![]() ,
, ![]() 两点.
两点.
(1)求抛物线的标准方程;
(2)如果直线![]() 过抛物线的焦点,求
过抛物线的焦点,求![]() 的值;
的值;
(3)如果![]() ,直线
,直线![]() 是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com