
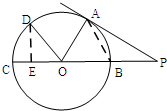
 如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转600到OD,则PD的长为( )
如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转600到OD,则PD的长为( ) 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
 A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是
A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是查看答案和解析>>
科目:高中数学 来源: 题型:
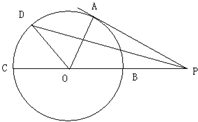 选修4-1:几何证明选讲
选修4-1:几何证明选讲| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为
A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为| 1 |
| 3 |
| 1 |
| 3 |
| 7 |
| 7 |
|
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省高三第四次模拟考试理科数学 题型:解答题
(.选修4—1:几何证明选讲
如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转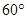 到O D.
到O D.
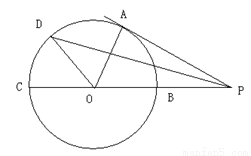
(1)求线段PD的长;
(2)在如图所示的图形中是否有长度为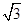 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com