
ЁОЬтФПЁПФГЕиЧј2009ФъжС2015ФъХЉДхОгУёМвЭЅШЫОљДПЪеШыyЃЈЕЅЮЛЃКЧЇдЊЃЉЕФЪ§ОнШчБэЃК
ФъЗн | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
ФъЗнДњКХt | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
ШЫОљДПЪеШыy | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
ЃЈ1ЃЉЧѓyЙигкtЕФЯпадЛиЙщЗНГЬЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌЗжЮі2009ФъжС2015ФъИУЕиЧјХЉДхОгУёМвЭЅШЫОљДПЪеШыЕФБфЛЏЧщПіЃЌВЂдЄВтИУЕиЧј2017ФъХЉДхОгУёМвЭЅШЫОљДПЪеШыЃЎ
ИНЃКЛиЙщжБЯпЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊЃК 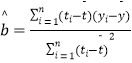 ЃЎ
ЃЎ ![]() ЃЎ
ЃЎ
ВЮПМЪ§ОнЃКЃЈЉ3ЃЉЁСЃЈЉ1.4ЃЉ+ЃЈЉ2ЃЉЁСЃЈЉ1ЃЉ+ЃЈЉ1ЃЉЁСЃЈЉ0.7ЃЉ+1ЁС0.5+2ЁС0.9+3ЁС1.6=14ЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКгЩЫљИјЪ§ОнМЦЫуЕУ
![]() =
= ![]() =4ЃЌ
=4ЃЌ
![]() =
= ![]() =4.4ЃЌ
=4.4ЃЌ
ЃЈtiЉ ![]() ЃЉ2=9+4+1+0+1+4+9=28ЃЌ
ЃЉ2=9+4+1+0+1+4+9=28ЃЌ
![]() ЃЈtiЉ
ЃЈtiЉ ![]() ЃЉЃЈyiЉ
ЃЉЃЈyiЉ ![]() ЃЉ=ЃЈЉ3ЃЉЁСЃЈЉ1.4ЃЉ+ЃЈЉ2ЃЉЁСЃЈЉ1ЃЉ+ЃЈЉ1ЃЉЁСЃЈЉ0.7ЃЉ+1ЁС0.5+2ЁС0.9+3ЁС1.6=14ЃЎЃЌ
ЃЉ=ЃЈЉ3ЃЉЁСЃЈЉ1.4ЃЉ+ЃЈЉ2ЃЉЁСЃЈЉ1ЃЉ+ЃЈЉ1ЃЉЁСЃЈЉ0.7ЃЉ+1ЁС0.5+2ЁС0.9+3ЁС1.6=14ЃЎЃЌ
 =
= ![]() =0.5ЃЌ
=0.5ЃЌ ![]() =4.3Љ0.5ЁС4=2.3ЃЌ
=4.3Љ0.5ЁС4=2.3ЃЌ
ЫљЧѓЛиЙщЗНГЬЮЊy=0.5t+2.3
ЃЈ2ЃЉНтЃКгЩЃЈ1ЃЉжЊЃЌb=0.5ЃО0ЃЌЙЪ2009ФъжС2015ФъИУЕиЧјОгУёМвЭЅШЫОљДПЪеШыж№ФъдіМгЃЌЦНОљУПФъдіМг0.5ЧЇдЊЃЎ
НЋ2017ФъЕФФъЗнДњКХt=9ДњШыЃЈ1ЃЉЕФЛиЙщЗНГЬЃЌЕУy=6.8ЃЌ
ЙЪдЄВтИУЕиЧј2017ФъИУЕиЧјОгУёМвЭЅШЫОљДПЪеШыдМЮЊ6.8ЧЇдЊЃЎ
ЁОНтЮіЁПЃЈ1ЃЉЯШЧѓГіФъЗнДњКХtКЭШЫОљДПЪеШыyЕФЦНОљЪ§ЃЌЕУЕНетзщЪ§ОнЕФбљБОжааФЕуЃЌРћгУзюаЁЖўГЫЗЈЧѓГіЯпадЛиЙщЗНГЬЕФЯЕЪ§ЃЌДњШыбљБОжааФЕуЧѓГіaЕФжЕЃЌаДГіЯпадЛиЙщЗНГЬЃЛЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃЌb=0.5ЃО0ЃЌ2009ФъжС2015ФъИУЕиЧјОгУёМвЭЅШЫОљДПЪеШыж№ФъдіМгЃЌЦНОљУПФъдіМг0.5ЧЇдЊЃЌЧѓЕУ2017ФъЕФФъЗнДњКХt=9ДњШыЃЈ1ЃЉЕФЛиЙщЗНГЬЃЌЕУyЕФжЕЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшХзЮяЯпy2=2xЕФНЙЕуЮЊFЃЌЙ§ЕуMЃЈ ![]() ЃЌ0ЃЉЕФжБЯпгыХзЮяЯпЯрНЛгкAЃЌBСНЕуЃЌгыХзЮяЯпЕФзМЯпЯрНЛгкCЃЌ|BF|=2ЃЌдђЁїBCFКЭЁїACFЕФУцЛ§жЎБШЮЊ ЃЎ
ЃЌ0ЃЉЕФжБЯпгыХзЮяЯпЯрНЛгкAЃЌBСНЕуЃЌгыХзЮяЯпЕФзМЯпЯрНЛгкCЃЌ|BF|=2ЃЌдђЁїBCFКЭЁїACFЕФУцЛ§жЎБШЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁОЯњФГЩЬЦЗЃЌИљОнвдЭљзЪСЯЭГМЦЃЌЙЫПЭВЩгУЕФИЖПюЦкЪ§![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
ЩЬГЁОЯњИУЩЬЦЗЃЌПЩВЩгУВЛЭЌаЮЪНЕФЗжЦкИЖПюЃЌИЖПюЕФЦкЪ§![]() ЃЈЕЅЮЛЃК
ЃЈЕЅЮЛЃК ![]() ЃЉгыЩЬГЁОЯњвЛМўЩЬЦЗЕФРћШѓ
ЃЉгыЩЬГЁОЯњвЛМўЩЬЦЗЕФРћШѓ![]() ЃЈЕЅЮЛЃКдЊЃЉТњзуШчЯТЙиЯЕЃК
ЃЈЕЅЮЛЃКдЊЃЉТњзуШчЯТЙиЯЕЃК 
ЃЈЂёЃЉШєМЧЪТМўЁАЙКТђИУЩЬЦЗЕФ3ЮЛЙЫПЭжаЃЌжСЩйга1ЮЛВЩгУвЛДЮадШЋЖюИЖПюЗНЪНЁБЮЊ![]() ЃЌЪдЧѓЪТМў
ЃЌЪдЧѓЪТМў![]() ЕФИХТЪ
ЕФИХТЪ![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЧѓЩЬГЁОЯњвЛМўЩЬЦЗЕФРћШѓ![]() ЕФЗжВМСаМАЦкЭћ
ЕФЗжВМСаМАЦкЭћ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃгЮдАЛюЖЏгаетбљвЛИігЮЯЗЯюФПЃКМзЯфзгРязАга3ИіАзЧђЁЂ2ИіКкЧђЃЎввЯфзгРязАга1ИіАзЧђЁЂ2ИіКкЧђЃЎУПДЮгЮЯЗДгетСНИіЯфзгРяЫцЛњУўГі2ИіЧђЃЌШєУўГіЕФАзЧђВЛЩйгк2ИіЃЌдђЛёНБЃЎЃЈУПДЮгЮЯЗНсЪјКѓНЋЧђЗХЛидЯфЃЉ
ЃЈ1ЃЉЧѓдк1ДЮгЮЯЗНсЪјКѓЃЌЂйУўГі3ИіАзЧђЕФИХТЪЃПЂкЛёНБЕФИХТЪЃП
ЃЈ2ЃЉЧѓдк2ДЮгЮЯЗжаЛёНБДЮЪ§XЕФЗжВМСаМАЪ§бЇЦкЭћEЃЈXЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГАр![]() УћбЇЩњдквЛДЮзјЮЛЬхЧАЧќВтЪджаЃЌГЩМЈШЋВПНщгк
УћбЇЩњдквЛДЮзјЮЛЬхЧАЧќВтЪджаЃЌГЩМЈШЋВПНщгк![]() гы
гы![]() жЎМфЃЌНЋВтЪдНсЙћАДШчЯТЗНЪНЗжГЩЮхзщЃКЕквЛзщ
жЎМфЃЌНЋВтЪдНсЙћАДШчЯТЗНЪНЗжГЩЮхзщЃКЕквЛзщ![]() ЃЌЕкЖўзщ
ЃЌЕкЖўзщ![]() ЃЌЁЃЌЕкЮхзщ
ЃЌЁЃЌЕкЮхзщ![]() ЃЌЯТЭМЪЧАДЩЯЪіЗжзщЗНЗЈЕУЕНЕФЦЕТЪЗжВМжБЗНЭМЃЎ
ЃЌЯТЭМЪЧАДЩЯЪіЗжзщЗНЗЈЕУЕНЕФЦЕТЪЗжВМжБЗНЭМЃЎ
ЃЈЂёЃЉШєГЩМЈДѓгкЛђЕШгк![]() ЧваЁгк
ЧваЁгк![]() ШЯЮЊСМКУЃЌЧѓИУАрдкетДЮзјЮЛЬхЧАЧќВтЪджаГЩМЈСМКУЕФШЫЪ§ЃЛ
ШЯЮЊСМКУЃЌЧѓИУАрдкетДЮзјЮЛЬхЧАЧќВтЪджаГЩМЈСМКУЕФШЫЪ§ЃЛ
ЃЈЂђЃЉШєГЩМЈжЎВюЕФОјЖджЕДѓгк![]() ШЯЮЊСНЮЛбЇЩњЕФЩэЬхШЭЖШДцдкУїЯдВювьЃЎЯжДгЕквЛЁЂЮхзщжаЫцЛњШЁГіСНИіГЩМЈЃЌЧѓетСНЮЛбЇЩњЕФЩэЬхШЭЖШДцдкУїЯдВювьЕФИХТЪЃЎ
ШЯЮЊСНЮЛбЇЩњЕФЩэЬхШЭЖШДцдкУїЯдВювьЃЎЯжДгЕквЛЁЂЮхзщжаЫцЛњШЁГіСНИіГЩМЈЃЌЧѓетСНЮЛбЇЩњЕФЩэЬхШЭЖШДцдкУїЯдВювьЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊМьбщКЎМйбЇЩњзджїбЇЯАЕФаЇЙћЃЌФъМЖВПЖдФГАр50УћбЇЩњИїПЦЕФМьВтГЩМЈНјааСЫЭГМЦЃЌЯТУцЪЧеўжЮГЩМЈЕФЦЕТЪЗжВМжБЗНЭМЃЌЦфжаГЩМЈЗжзщЧјМфЪЧЃК ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓЭМжаЕФ![]() жЕМАЦНОљГЩМЈЃЛ
жЕМАЦНОљГЩМЈЃЛ
ЃЈ2ЃЉДгЗжЪ§дк![]() жабЁ5ШЫМЧЮЊ
жабЁ5ШЫМЧЮЊ![]() ЃЌДгЗжЪ§дк
ЃЌДгЗжЪ§дк![]() жабЁ3ШЫЃЌМЧЮЊ
жабЁ3ШЫЃЌМЧЮЊ![]() ЃЌ8ШЫзщГЩвЛИібЇЯАаЁзщЃЎЯжДгет5ШЫКЭ3ШЫжаИїбЁ1ШЫзіЮЊзщГЄЃЌЧѓ
ЃЌ8ШЫзщГЩвЛИібЇЯАаЁзщЃЎЯжДгет5ШЫКЭ3ШЫжаИїбЁ1ШЫзіЮЊзщГЄЃЌЧѓ![]() БЛбЁжаЧв
БЛбЁжаЧв![]() ЮДБЛбЁжаЕФИХТЪЃЎ
ЮДБЛбЁжаЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфЖЈвхгђЮЊ
ЃЌЦфЖЈвхгђЮЊ![]() ЃЈ
ЃЈ![]() ЃЉ,Щш
ЃЉ,Щш![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЪдШЗЖЈ![]() ЕФШЁжЕЗЖЮЇ,ЪЙЕУКЏЪ§
ЕФШЁжЕЗЖЮЇ,ЪЙЕУКЏЪ§![]() дк
дк![]() ЩЯЮЊЕЅЕїКЏЪ§ЃЛ
ЩЯЮЊЕЅЕїКЏЪ§ЃЛ
ЃЈЂђЃЉЪдХаЖЯ![]() ЕФДѓаЁВЂЫЕУїРэгЩЃЎ
ЕФДѓаЁВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇНёФъЧАЮхИідТУПдТЩњВњФГжжВњЦЗЕФЪ§СПCЃЈМўЃЉЙигкЪБМфtЃЈдТЃЉЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌдђетИіЙЄГЇЖдетжжВњЦЗРДЫЕЃЈЁЁЁЁЃЉ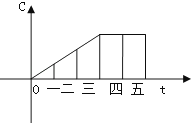
A.вЛжСШ§дТУПдТЩњВњЪ§СПж№дТдіМгЃЌЫФЁЂЮхСНдТУПдТЩњВњЪ§СПж№дТМѕЩй
B.вЛжСШ§дТУПдТЩњВњЪ§СПж№дТдіМгЃЌЫФЁЂЮхдТУПдТЩњВњЪ§СПгыШ§дТГжЦН
C.вЛжСШ§дТУПдТЩњВњЪ§СПж№дТдіМгЃЌЫФЁЂЮхСНдТОљЭЃжЙЩњВњ
D.вЛжСШ§дТУПдТЩњВњЪ§СПВЛБфЃЌЫФЁЂЮхСНдТОљЭЃжЙЩњВњ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУМђЕЅЫцЛњГщбљЗНЗЈДгКЌга6ИіИіЬхЕФзмЬхжаЃЌГщШЁвЛИіШнСПЮЊ2ЕФбљБОЃЌФГвЛИіЬхaЁАЕквЛДЮБЛГщЕНЕФИХТЪЁБЁЂЁАЕкЖўДЮБЛГщЕНЕФИХТЪЁБЁЂЁАдкећИіГщбљЙ§ГЬжаБЛГщЕНЁБЕФИХТЪЗжБ№ЪЧ
ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com