
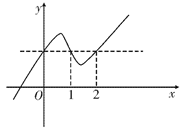
 函数y=f(x)的图象如右图所示,且函数y=F(x)的图象经过(1,2)和(-1,2)两点,又过点(1,0)作斜率之积为-10的两条直线l1和l2,l1和l2与函数
函数y=f(x)的图象如右图所示,且函数y=F(x)的图象经过(1,2)和(-1,2)两点,又过点(1,0)作斜率之积为-10的两条直线l1和l2,l1和l2与函数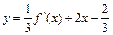 的图象分别相交于A、B两点和C、D两点,O为坐标原点。
的图象分别相交于A、B两点和C、D两点,O为坐标原点。 ≥
≥
 , 2分
, 2分



 6(m-1)3="0 "
6(m-1)3="0 "  m=1
m=1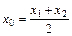 ∴
∴ ,
, ,
, >0
>0  k>4或k<0 ①
k>4或k<0 ① ,同理有kx2+10x-10="0 " 8分
,同理有kx2+10x-10="0 " 8分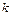 >
> ②
② <k<0或k>4 由上可知
<k<0或k>4 由上可知 ,
,
 ,
,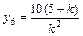 ∵
∵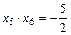 <0,∴M,N两点在y轴的两侧.
<0,∴M,N两点在y轴的两侧. =
=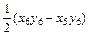 ,
,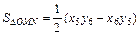
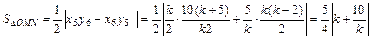 , 11分
, 11分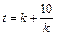 ,由双勾函数的性质可知,在
,由双勾函数的性质可知,在 <k<0或k>4时,
<k<0或k>4时,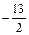 或t≥
或t≥ ∴|t|≥
∴|t|≥ ∴
∴ ≥
≥ 13分
13分

科目:高中数学 来源:不详 题型:解答题
 (
( ),其中
),其中 .(Ⅰ)当
.(Ⅰ)当 时,讨论函数
时,讨论函数 的单调性;(Ⅱ)若函数
的单调性;(Ⅱ)若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围;(Ⅲ)若对于任意的
的取值范围;(Ⅲ)若对于任意的 ,不等式
,不等式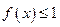 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R). 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com