
(本小题满分12分)
某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第一组 [160,164],第二组[164,168],…,第6组[180,184],下图是按上述分组方法得到的频率分布直方图.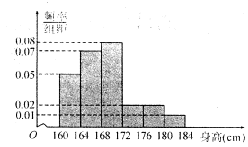
(Ⅰ)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(Ⅱ)求这50名男生身高在172 cm以上(含172 cm)的人数;
(Ⅲ)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为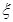 ,求
,求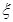 的数学期望.
的数学期望.
参考数据:
若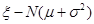 .则
.则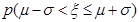 =0.6826,
=0.6826,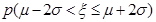 ="0.9544,"
="0.9544," 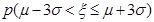 =0.9974.
=0.9974.
(Ⅰ)高于全市的平均值168。
(Ⅱ)这50名男生身高在172 cm以上(含172 cm)的人数为10人.
(Ⅲ)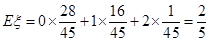
解析试题分析:(Ⅰ)由直方图,经过计算该校高三年级男生平均身高为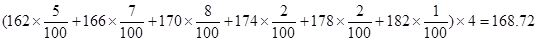 ,
,
高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168). …………………………………………………………(4分)
(Ⅱ)由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×5=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10人. ……………(6分)
(Ⅲ)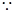
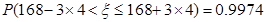 ,
,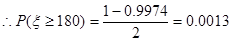 ,0.0013×100 000=130.
,0.0013×100 000=130.
所以,全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量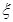 可取
可取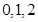 ,于是
,于是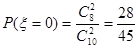 ,
,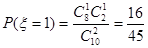 ,
,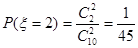
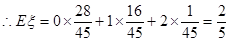 . …………………(12分)
. …………………(12分)
考点:本题主要考查离散性随机变量的分布列及数学期望。
点评:本题是对频率、频数灵活运用的综合考查,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率= .涉及组合数计算要细心。
.涉及组合数计算要细心。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属醉酒驾车,对于酒后驾车和醉酒驾车的驾驶员公安机关将给予不同程度的处罚.
某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了250辆机动车,查出酒后
驾车和醉酒驾车的驾驶员20人,下图是对这20人血液中酒精含量进行检查所得结果的频率分布
直方图.
(1)根据频率分布直方图,求此次抽查的250人中,醉酒驾车的人数;
(2)从血液酒精浓度在[70,90)范围内的驾驶员中任取2人,求恰有1人属于醉酒驾车的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):
甲班
| 成绩 | 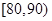 |  | 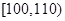 | 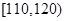 | 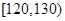 |
| 频数 | 4 | 20 | 15 | 10 | 1 |
| 成绩 | 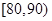 |  | 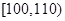 | 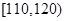 | 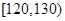 |
| 频数 | 1 | 11 | 23 | 13 | 2 |
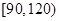 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;| | 成绩小于100分 | 成绩不小于100分 | 合计 |
| 甲班 | 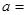 | 26 | 50 |
| 乙班 | 12 | 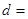 | 50 |
| 合计 | 36 | 64 | 100 |
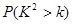 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
驾驶员血液酒精浓度在20~80 mg/100 mL(不含80)之间,属酒后驾车,血液酒精浓度在80 mg/100 mL(含80)以上时,属醉酒驾车.市交警一队对过往的车辆进行抽查共查出喝过酒的驾车者60名,下图是这60名驾车者血液中酒精浓度的频率分布直方图.
(1) 求这60名驾车者中属醉酒驾车的人数;(图中每组包括左端点,不包括右端点)
(2) 求这60名驾车者血液的酒精浓度的平均值;
(3) 将频率分布直方图中的七组从左到右依次命名为第一组,第二组,…,第七组,在第五组和第七组的所有人中抽出两人,记他们的血液酒精浓度分别为x,y(单位: mg/100 ml),则事件|x-y|≤10的概率是多少?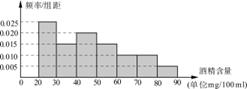
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有1000名学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表和频数分布条形图,解答下列问题:
(1)求频率分布表中的 ,
,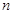 值,并补全频数条形图;
值,并补全频数条形图;
(2)根据频数条形图估计该样本的中位数是多少?
(3)若成绩在65.5~85.5分的学生为三等奖,问该校获得三等奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
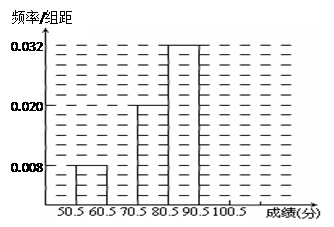
(本小题满分12分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 6 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 15 | |
| 80.5~90.5 | 24 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 75 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附: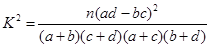 ;
;
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下: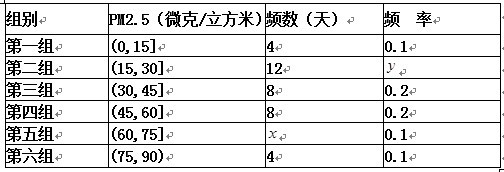
(1)试确定x,y的值,并写出该样本的众数和中位数(不必写出计算过程);
(2)完成相应的频率分布直方图.
(3)求出样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: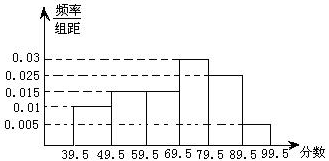
(1)79.5到89.5这一组的频率、频数分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格).
(3)估计这次环保知识竞赛的平均分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com