
分析 首先根据一元二次方程求出α+β=$\sqrt{10}$,α•β=2,进一步对关系式$\frac{{α}^{2}-αβ+{β}^{2}}{(α-β)^{2}}$进行恒等变换,最后求出结果.
解答 解:α、β是方程x2-$\sqrt{10}$x+2=0的两实根,
则:α+β=$\sqrt{10}$,α•β=2.
故:$\frac{{α}^{2}-αβ+{β}^{2}}{(α-β)^{2}}$=$\frac{(α+β)^{2}-3αβ}{(α+β)^{2}-4αβ}$=2,
则:$lo{g}_{2}\frac{{α}^{2}-αβ+{β}^{2}}{(α-β)^{2}}$=1.
点评 本题考查的知识要点:一元二次方程的根和系数的关系,对数的运算和式子的恒等变形问题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{17}{4}$ | D. | $\frac{15}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,$\frac{3}{4}$] | B. | [-$\frac{3}{4}$,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,-$\frac{1}{4}$] | D. | [$\frac{1}{4}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
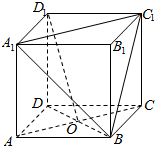 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{3}$,π) | B. | ($\frac{π}{3}$,π] | C. | [$\frac{π}{3}$,π] | D. | (0,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com