
【题目】如图,已知等边![]() 中,
中,![]() 分别为
分别为![]() 边的中点,
边的中点,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 边上一点,且
边上一点,且![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,使平面
的位置,使平面![]() 平面EFCB.
平面EFCB.
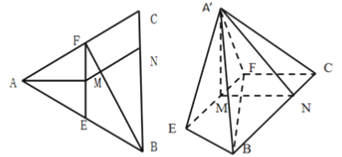
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)证明A'M⊥EF,推出A'M⊥平面EFCB,得到A'M⊥BF,证明BF⊥MN.得到BF⊥平面A'MN.然后证明平面A'MN⊥平面A'BF;
(2)设等边![]() 的边长为4,取
的边长为4,取![]() 中点
中点![]() ,连接
,连接![]() ,由题设知
,由题设知![]() ,由(1)知
,由(1)知![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,如图建立空间直角坐标系
,如图建立空间直角坐标系![]() ,利用两个平面的法向量的夹角即可得出.
,利用两个平面的法向量的夹角即可得出.
试题解析:
(I)因为![]() 为等边
为等边![]() 的
的![]() 边的中点,所以
边的中点,所以![]() 是等边三角形,且
是等边三角形,且![]() .因为
.因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又由于平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
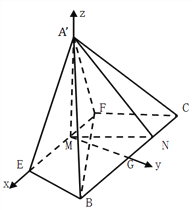
又![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
在正![]() 中知
中知![]() ,所以
,所以![]() .
.
而![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(II)设等边![]() 的边长为4,取
的边长为4,取![]() 中点
中点![]() ,
,
连接![]() ,由题设知
,由题设知![]() ,
,
由(I)知![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,如图建立空间直角坐标系
,如图建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则由
,则由
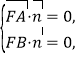 得
得![]() 令
令![]() ,则
,则![]() .
.
平面![]() 的一个法向量为
的一个法向量为![]()
所以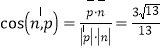 ,
,
显然二面角![]() 是锐角,所以二面角
是锐角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和
和![]() 的焦点分别为
的焦点分别为![]() ,
, ![]() 交于O,A两点(O为坐标原点),且
交于O,A两点(O为坐标原点),且![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点O的直线交![]() 的下半部分于点M,交
的下半部分于点M,交![]() 的左半部分于点N,点
的左半部分于点N,点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车租赁公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表:
A型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
B型车
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(1)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(2)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(3)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为 ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)求直线![]() 与曲线
与曲线![]() 的交点的直角坐标.
的交点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1, 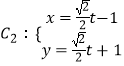 (t为参数).
(t为参数).
(Ⅰ)求曲线C1上的点到曲线C2距离的最小值;
(Ⅱ)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的 ![]() 倍,得到曲线
倍,得到曲线 ![]() .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 ![]() 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com