
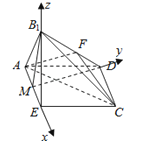
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC=![]() BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
BC=a,E是BC的中点,将△BAE沿AE折起到△B1AE的位置,使平面B1AE⊥平面AECD,F为B1D的中点.
(1)证明:B1E∥平面ACF;
(2)求平面ADB1与平面ECB1所成锐二面角的余弦值.
【答案】证明:(1)连结ED交AC于O,连结OF,
因为AECD为菱形,OE=OD,
所以FO∥B1E,
所以B1E∥平面ACF.
(2)取AE的中点M,连结B1M,连结MD,则∠AMD=90°,
分别以ME,MD,MB1为x,y,z轴建系,
则E(![]() ,0,0),C(a,
,0,0),C(a,![]() a,0),A(﹣
a,0),A(﹣![]() ,0,0),D(0,
,0,0),D(0,![]() a,0),
a,0),
B1(0,0,![]() a),
a),
则![]() =(﹣
=(﹣![]() ,0,
,0,![]() a),
a),![]() =(
=(![]() ,
,![]() a,0),
a,0),![]() =(
=(![]() ,0,
,0,![]() a),
a),
设面ECB1的法向量为![]() =(x,y,z),
=(x,y,z),
则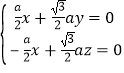 ,令x=1,则
,令x=1,则![]() =(1,﹣
=(1,﹣![]() ,
,![]() ),
),
同理面ADB1的法向量为![]() =(1,﹣
=(1,﹣![]() ,﹣
,﹣![]() )
)
所以cos<![]() ,
,![]() >=
>=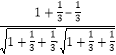 =
=![]() ,
,
故平面ADB1与平面ECB1所成锐二面角的余弦值为![]()
【解析】(1)根据线面平行的判定定理即可证明:B1E∥平面ACF;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可得到结论.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.


科目:高中数学 来源: 题型:
【题目】给出以下结论,其中正确结论的个数为( )
①函数![]() 的零点为
的零点为![]() ,则函数
,则函数![]() 的图象经过点
的图象经过点![]() 时,函数值一定变号.
时,函数值一定变号.
②相邻两个零点之间的所有函数值保持同号.
③函数![]() 在区间
在区间![]() 上连续,若满足
上连续,若满足![]() ,则方程
,则方程![]() 在区间
在区间![]() 上一定有实根.
上一定有实根.
④“二分法”对连续不断的函数的所有零点都有效.
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱ABCD-A1B1C1D1中,![]() ,平面BB1C1C
,平面BB1C1C![]() 底面ABCD,点
底面ABCD,点![]() 、F分别是线段
、F分别是线段![]() 、BC的中点.
、BC的中点.
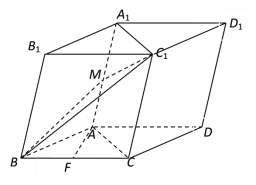
(1)求证:AF//平面![]() ;
;
(2)求证:平面BB1C1C⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月19日,由中国工信部、江西省政府联合主办的世界VR(虚拟现实)产业大会在南昌开幕,南昌在红谷滩新区建立VR特色小镇项目.现某厂商抓住商机在去年用450万元购进一批VR设备,经调试后今年投入使用,计划第一年维修、保养费用22万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为180万元,设使用x年后设备的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)使用若干年后,当年平均盈利额达到最大值时,求该厂商的盈利额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线![]() 的参数方程为
的参数方程为![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每![]() 枚的市场价
枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 |
|
|
|
市场价 |
|
|
|
(1)根据上表数据,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系:①
的变化关系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格;
(3)设你选取的函数为![]() ,若对任意实数
,若对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 恒有个想异实数根,求
恒有个想异实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其图像的一个对称中心是
其图像的一个对称中心是![]() 将
将![]() 的图像向左平移
的图像向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像。
的图像。
(1)求函数![]() 的解析式;
的解析式;
(2)若对任意![]() 当
当![]() 时,都有
时,都有![]() 求实数
求实数![]() 的最大值;
的最大值;
(3)若对任意实数![]() 在
在![]() 上与直线
上与直线![]() 的交点个数不少于6个且不多于10个,求正实数
的交点个数不少于6个且不多于10个,求正实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com