
【题目】已知双曲线![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,点P为双曲线C右支上异于顶点的一点,
,点P为双曲线C右支上异于顶点的一点,![]() 的内切圆与x轴切于点
的内切圆与x轴切于点![]() ,且直线
,且直线![]() 经过线段
经过线段![]() 的中点且垂直于线段
的中点且垂直于线段![]() ,则双曲线C的方程为________________.
,则双曲线C的方程为________________.
【答案】![]()
【解析】
设点![]() 是双曲线右支上一点,由双曲线的定义,知
是双曲线右支上一点,由双曲线的定义,知![]() ,设三角形
,设三角形![]() 的内切圆与
的内切圆与![]() 轴的切点为
轴的切点为![]() ,
,![]() 、
、![]() 分别为内切圆与
分别为内切圆与![]() 、
、![]() 的切点,由同一点向圆引得两条切线相等知
的切点,由同一点向圆引得两条切线相等知![]() ,由此得到
,由此得到![]() ,再利用直线
,再利用直线![]() 经过线段
经过线段![]() 的中点且垂直于线段
的中点且垂直于线段![]() ,设
,设![]() ,运用直线的斜率公式和中点在直线
,运用直线的斜率公式和中点在直线![]() 上,化简整理得
上,化简整理得![]() ,再利用双曲线的定义
,再利用双曲线的定义![]() ,得
,得![]() ,进而得到双曲线方程.
,进而得到双曲线方程.
点![]() 是双曲线右支上一点,由双曲线的定义,知
是双曲线右支上一点,由双曲线的定义,知![]() ,若设三角形
,若设三角形![]() 的内切圆与
的内切圆与![]() 轴的切点为
轴的切点为![]() ,
,![]() 、
、![]() 分别为内切圆与
分别为内切圆与![]() 、
、![]() 的切点,
的切点,
由同一点向圆引得两条切线相等知,且![]() ,
,![]()
则有![]() ,
,
所以![]() ,即
,即![]() ,
,
再设![]() ,
,![]() ,
,![]() ,则
,则![]() 的中点坐标为
的中点坐标为![]() ,
,![]() ,
,
由直线![]() 经过线段
经过线段![]() 的中点且垂直于线段
的中点且垂直于线段![]() ,
,
所以有![]() ,
,![]() ,整理得
,整理得![]() ,
,![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,又
,又![]() ,
,
所以![]() ,在双曲线中,
,在双曲线中,![]() ,
,
故双曲线方程为![]() .
.
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为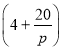 元
元![]() 件.
件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年辽宁省正式实施高考改革.新高考模式下,学生将根据自己的兴趣、爱好、学科特长和高校提供的“选考科目要求”进行选课.这样学生既能尊重自己爱好、特长做好生涯规划,又能发挥学科优势,进而在高考中获得更好的成绩和实现自己的理想.考改实施后,学生将在高二年级将面临着![]() 的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
的选课模式,其中“3”是指语、数、外三科必学内容,“1”是指在物理和历史中选择一科学习,“2”是指在化学、生物、地理、政治四科中任选两科学习.某校为了更好的了解学生对“1”的选课情况,学校抽取了部分学生对选课意愿进行调查,依据调查结果制作出如下两个等高堆积条形图:根据这两幅图中的信息,下列哪个统计结论是不正确的( )
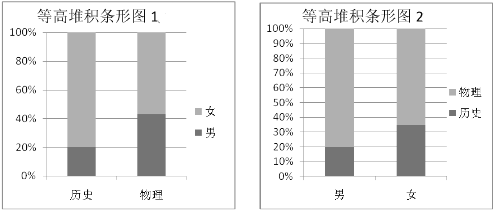
A.样本中的女生数量多于男生数量
B.样本中有学物理意愿的学生数量多于有学历史意愿的学生数量
C.样本中的男生偏爱物理
D.样本中的女生偏爱历史
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两条不同直线,
是两条不同直线,![]() ,
,![]() 是两个不同平面,给出下列四个命题:
是两个不同平面,给出下列四个命题:
①若![]() ,
,![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行;
平行;
②若![]() ,
,![]() 平行于同一平面,则
平行于同一平面,则![]() 与
与![]() 平行;
平行;
③若![]() ,
,![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线;
平行的直线;
④若![]() ,
,![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂因排污比较严重,决定着手整治,一个月时污染度为![]() ,整治后前四个月的污染度如下表:
,整治后前四个月的污染度如下表:
月数 |
|
|
|
| … |
污染度 |
|
|
|
| … |
污染度为![]() 后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:![]() ,
,![]() ,
,![]() ,其中
,其中![]() 表示月数,
表示月数,![]() 、
、![]() 、
、![]() 分别表示污染度.
分别表示污染度.
(1)问选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.有两个面相互平行,其余各面都是平行四边形的多面体是棱柱
B.正四面体是四棱锥
C.有一个面是多边形,其余各面都是三角形的多面体叫做棱锥
D.正四棱柱是平行六面体
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com