
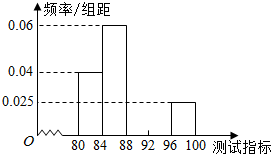
 某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:
某工厂将生产的某种芯片的质量按测试指标划分为五组(指标数值越大.产品质量越好),现随机抽取芯片50件进行检测.检测结果统计如下:| 组号 | 测试指标 | 频数 | 频率 |
| 第一组 | [80,84] | 8 | 0.16 |
| 第二组 | [84,88] | x | 0.24 |
| 第三组 | [88,92] | 15 | p |
| 第四组 | [92,96] | 10 | q |
| 第五组 | [96,100] | y | 0.1 |
| 合 计 | 50 | 1 | |
分析 (1)根据频率、频数与样本容量的关系,求出x、y与p、q的值,并补全频率分布直方图;
(2)根据第三、四、五组的频数求出抽取6件产品各组应抽取的产品数,编号后利用列举法求出基本事件数,再求出对应的概率.
解答 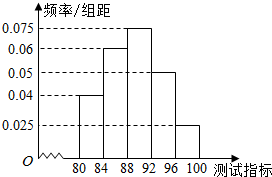 解:(1)根据题意,x=50×0.24=12,
解:(1)根据题意,x=50×0.24=12,
y=50×0.1=5,
p=$\frac{15}{50}$=0.3,
q=$\frac{10}{50}$=0.2;
补全频率分布直方图如下;
(2)第三、四、五组的频数分别为15、10和5,
用分层抽样法抽取6件产品,第三组抽3件,记为a、b、c,
第四组抽取2件,记为D、E,第五组抽取1件,记为f;
从这6件中选2件,基本事件是
ab、ac、aD、aE、af、bc、bD、bE、bf、cD、cE、cf、DE、Df、Ef共15种,
2件产品中至少有1件来自第四组的基本事件是
aD、aE、bD、bE、cD、cE、DE、Df、Ef共9种;
所以所求的概率为P=$\frac{9}{15}$=0.6.
点评 本题考查了频率分布直方图的应用问题,也考查了分层抽样方法与列举法求古典概型的概率问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
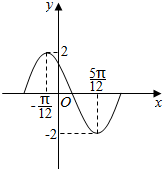 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为y=2sin(2x+$\frac{2π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.
如图,一根长为2米的竹竿AB斜靠在在直角墙壁上,假设竹竿在同一平面内移动,当竹竿的下段点A从距离墙角O点1米的地方移动到$\sqrt{3}$米的地方,则AB的中点D经过的路程为$\frac{π}{6}$米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com